水の融点や沸点について調べてみると「正確には水は99.974℃で沸騰する」といった文言をよく見かけるので、実際のところはどうなっているのか調べてみました。
沸点と融点の話はとっても単純に見えるのに、厳密に考えるのは思った以上にずっと難しいみたいで色々と学んだことがあったのでそれらをメモしました。
記載の内容を参照する際は十分にお気をつけください
要約
- 水の融点・沸点の温度は圧力に依存する → 標準気圧であることが前提
- 水の同位体組成にも依存する → 同位体標準のVSMOWという純水が用いられる
- 現在の温度の定義では、水の融点はピッタリ0℃でない (沸点も100℃ではない)
- 融点:0.002519 ℃, 沸点:99.974 ℃ 。でも実はこれ、測定値ではなく計算値
- 水の融点や沸点は状態方程式から計算によって決定された値
水の融点・沸点の前提条件 (~大前提編~)
「水は○○℃で沸騰する」という一文にも実は色々な条件が前提として隠されている。
その中でも「当たり前」とみなせるような大大大前提は次の通り。
水は不純物を含まない「純水」である
水に別の物質が溶解していると融点や沸点は変化する。
例えば水に食塩(NaCl)を溶解させると融点が下がり、0℃でも凍らなくなる例が有名。(凝固点降下)
ちなみにこの食塩水の沸点は100℃よりも高くなる。(沸点上昇)
純物質としての水の融点や沸点なので、前提として不純物を含まない(可能な限り少ない)水であるとする。
(普段使っている水道水のような水はもちろん純水でない。)
で、実際にはこの「純水」が厳密には1種類ではない (更に細かい条件が必要)というのが見落としがちながら重要な点なので後述。
水の状態は「温度」「圧力」の2つに依存する
「○○℃で沸騰する」という文言では省略されがちだが、温度だけでなく圧力も指定しなければ水の状態は1つに定まらない。
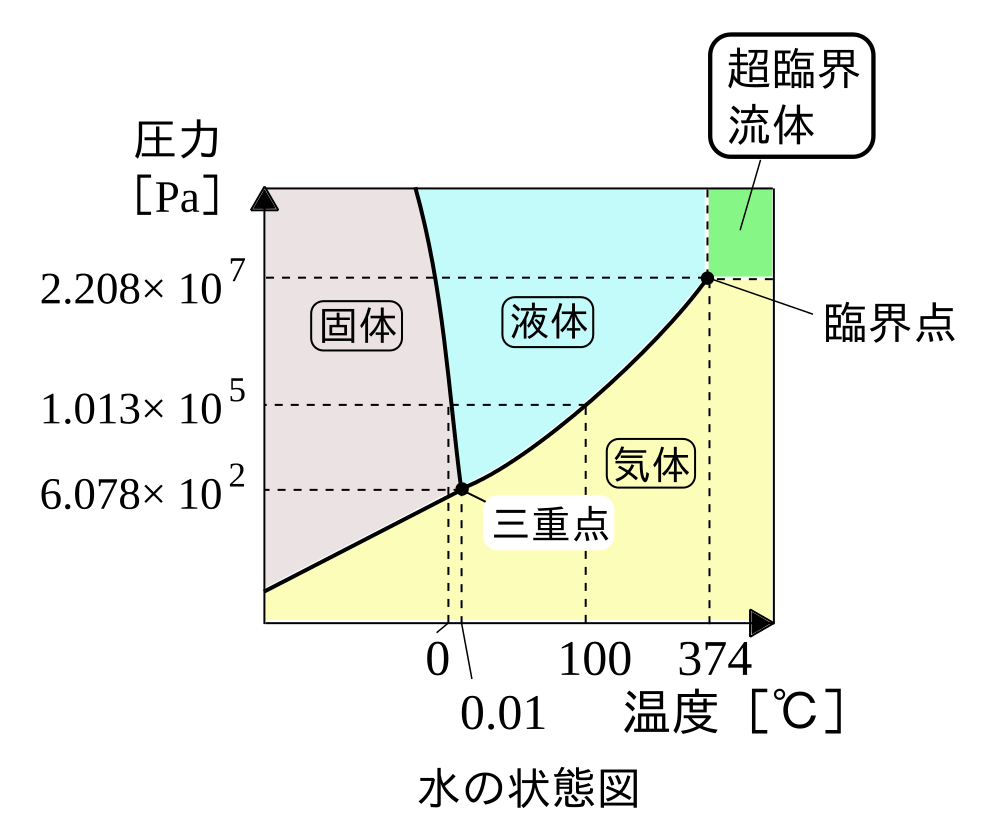
※この状態図の解説はこちら→ 高等学校化学II/物質の三態
水の状態図(相図)を見ると分かりやすいが、水が固体・液体・気体のどの状態を取るかは温度と圧力の両方に依存する。
例えば富士山の山頂のような圧力(気圧)の低い場所で水を沸かそうとすると 100℃よりも低い温度で沸騰する。
上の状態図で見れば、圧力が1気圧 (約 1.013×105 Pa) よりも低いとき、右側の曲線(蒸気圧曲線)で圧力に対応する温度も低くなっている。(つまり沸点が低くなっている)
「水は100℃で沸騰する」という文言では、圧力の指定:1気圧 (約 1.013×105 Pa) が省略されていることに注意。
正確な圧力の指定
圧力は明記した方が良いと思うが、特に断り書きのない場合は標準気圧 (正確に 101325 Pa)として扱う。
すなわち、1 気圧は正確に 1.01325×105 Pa である。
(もちろん日常生活の中で自分たちがいる場所の気圧は標準気圧から基本的にずれているだろうし、一定でもない)
以下、これまでに書いた大前提よりも細かい色々な条件について記載。
条件:水分子を構成する水素原子・酸素原子の同位体比
厳密には、融点と沸点は水分子(H2O)を構成する水素原子(H)・酸素原子(O)の同位体比に依存する。
各同位体ごと質量が異なるため、異なる同位体の水素原子・酸素原子の組から成る水分子は同じ「水」であっても融点や沸点といった物理的性質に違いを生じる。
(水素原子と酸素原子それぞれの同位体一覧はこちら → 水素の同位体 / 酸素の同位体 )
したがって、特定の同位体組成の水を指定しなければ (同じ「純水」であっても) 融点や沸点は一つに定まらない。
幸いにも同位体組成の基準となる同位体標準としてウィーン標準平均海水(VSMOW)があり、これが水の融点・沸点の決定に使われる「純水」である。
(海水と名前についているが塩や不純物を含まない純水。)
VSMOWの同位体組成や詳細については上記リンク参照。以下、「水」という言葉はVSMOWを指すものとして進める。
条件を省略した文言 → 条件を明記した文言
いや普段目にする水の沸点の記述にこういう前提条件が含まれてたなんて初見じゃ分からないでしょ!!!(おこ!😾)
条件:用いた温度の定義
水が100℃で沸騰する時代は終わった?!
さすがにここまで厳密に「水」を指定すれば融点と沸点を決められそうだが、実際にはまだ注意しなければならない別の条件が存在する。
それが、融点や沸点に用いる温度の定義。
実は「水の融点を0℃、沸点を100℃」とするセルシウス温度の定義は既に廃止されていて、現在の定義では水の融点と沸点が変わっている。
0℃ピッタリ・100℃ピッタリの時代は終わった模様。
現在、水の融点や沸点の「温度」の定義として用いられているのは1990年国際温度目盛(ITS-90)で定義された国際ケルビン温度(単位:K)や国際セルシウス温度(単位:℃)となっている。
(出典は後述。定義の中身についても後述)
それらの定義は「水の融点を0℃・沸点を100℃とする」といった古典的なセルシウス温度の定義とは異なる別の方法に基づく温度定義なので、もちろん水の融点や沸点も0℃・100℃から変わってくる。
気になる水の融点・沸点は…
上記のITS-90で定義された国際セルシウス温度と国際ケルビン温度による、水(VSMOW)の標準気圧における融点・沸点は
沸点:99.974 ℃ (373.124 K)
である"らしい"。 ここで問題発生。よく見かける中途半端な融点・沸点の値の謎が解けたので後は出典を調べるだけ! となったのだが、なかなか出典が見つからない…。
各論文やWikipediaに載っているこれらの値が一体どこから来て、どんな方法で得られた測定値なのか全く分からない状態…。
→ 出典を探しているうちに更に細かいことについても学べたので、次の大項目以降にまとめた。(肝心の出典も後述)
ITS-90 の詳細について
本来はITS-90の公式文書(フランス語)または公式の英語版テキストを参照すべきだが、フランス語読めない&時間の制約上、日本語訳を参照した。
これは日本の計量研究所が、国際度量衡局から出版された公式の仏文・英文文書を基に日本語に訳したもの。
読むにあたってこちらも参考にした。(上記文書も下記補足資料も1990年代のものであり、現在とは異なる記述があるので注意。)
(※国際ケルビン温度[K] と 国際セルシウス温度[℃] の関係)
2つには次の関係が成り立つ。(定義)
273.15 はだいたいの値ではなく、正確に 273.15 であることに注意。
(例えば 0 ℃ は正確に 273.15 K で、100 ℃ は 正確に 373.15 K)
また、この関係からも分かるように 1℃ の上昇幅と 1K の上昇幅は全く同じ。
(ちなみにこれが国際セルシウス温度の定義式(とほぼ同じ記述。) 国際ケルビン温度の定義は後述。)
水の融点と沸点はどのように決定されたのか
結論 (要約)
- 融点 0.002519 ℃ と 沸点 99.974 ℃ の値は直接融点・沸点を測定した値ではなく、計算値。
- 融点の方は、計算によって算出された融解曲線から得られた値。
- 沸点も計算により算出された値。
(調べるまで私は精密な測定で直接融点や沸点を調べているものだと勝手に思っていました…。計算値だったんですね…!!)
ㅤ
水の融点について
国際水・蒸気性質協会 (IAPWS) の文書:Revised Release on the Equation of State 2006 for H2O Ice Ih の p.8 を見ると、水の融点について
- 温度は ITS-90 に基づいている
- 氷と水の相平衡状態の評価により熱力学的に整合した融解曲線が算出される
- 氷と水の相平衡状態の評価には計算が用いられている (※1)
- この方法で、常圧(標準気圧)での融解温度の値 273.152519 K をわずか 2μK (=0.000002 K) の不確かさで決定できた (※2)
という記載があった。
(※1) 融解曲線の算出方法について
文書(p.8, 5章) には「氷と水の相平衡状態 (g = gL、gは式(1)から計算、gL は IAPWS-95 [7] から計算)」という記載があったので、文書 p.4 の式(1) と IAPWS-95 の2つの式から融解曲線を算出しているようだ。
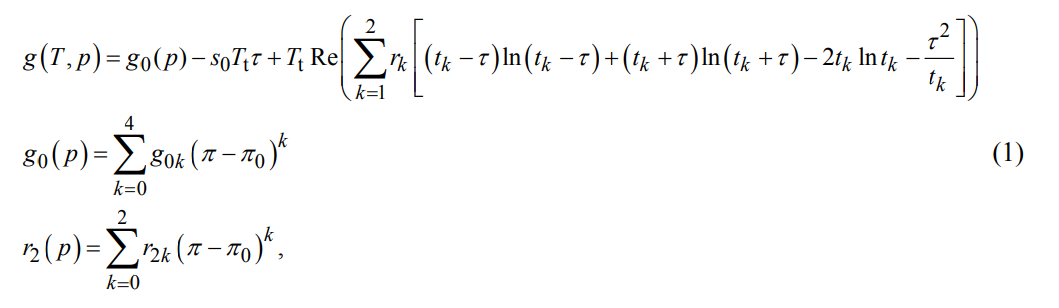
Feistel, Rainer & Wagner, Wolfgang. (2006). A new equation of state for H2O Ice Ih. Journal of Physical and Chemical Reference Data. (p.4 の式(1)) を引用
式(1)は氷(固体)の Gibbsエネルギー g を 温度 T, 圧力 p で表した関数。(氷の状態方程式)
※各文字の意味や値については文書を参照。
そして、IAPWS-95 formulation は 水(液体)のGibbsエネルギーの式(状態方程式)みたいなので、この2つの式が等しくなるのは氷と水の両者でGibbsエネルギーが等しい状態、つまり氷と水が平衡状態にある場合となる。
2式を等号で結べば残る変数は T, p だけになるので、その式は T-p 平面上でおなじみの融解曲線を描く。
こうして融解曲線が計算により得られる、ということらしい。(※自分自身で計算を全く追っていないので、理解できていない部分が多々あり)
IAPWS-95 formulation
先ほどの文書の出典[7] The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use が有料で読めなかったので、肝心な IAPWS-95式を閲覧できなかった…。
→ 別の論文で式の掲載を確認。後述。
(※2) 融点の決定について
計算で融解曲線(の式)が得られたので、あとはそこから p が標準気圧のときの T の値を求めれば水の融点が求められる。
そのようにして求められた値が、T = 273.152519 [K] (0.002519 [℃])
その融点はわずか 2μK 不確かさで決定できたらしいが、その詳細について記載された論文(出典[1])が有料だったため中身を確認できていない。
論文[1]:A New Equation of State for H2O Ice Ih
なお、式(1)の状態方程式の開発に用いた氷Ih相の実験データに関する情報も上記論文に示されているらしい。
ㅤ
水の沸点について
IAPWS の文書:The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Useの p.395 (:右上ページ番号) を見ると、水の沸点について
Tb = 373.124 K
と記載されており、その隣には Eq. (6.4)c と書かれている。
注釈c には
cCalculated from IAPWS-95, Eq. (6.4), by solving the phase-equilibrium condition, Eqs. (6.9a) – (6.9c).
と書かれているので、沸点も(測定値ではなく)計算値のようだ。
(あれ…! 有料だったせいで先ほど見られず諦めていた IAPWS-95 式 が閲覧できそう…!!)
式(6.4) の IAPWS-95 式を見てみる。(p.429 ※PDFの43ページ目) 式(6.9a)~(6.9c)も。(p.431 ※PDFの45ページ目)
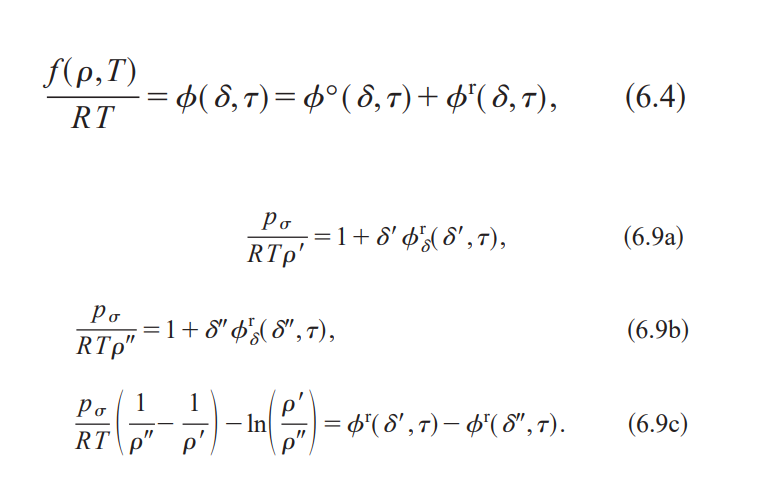
Wagner, W & Pruß, A. (2002). The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. Journal of Physical and Chemical Reference Data. (p.429 の式(6.4)、p. 431の式(6.9a)~(6.9c)) を引用
式の細かい中身は(先ほどと同様)、無学状態の私には追えない&分からないので申し訳ないですが省略。
こちらの式だと何をどう連立して p-T 間の関係(蒸気圧曲線)が得られるのか分からない…。
(地味に f はギブズエネルギーじゃなくてヘルムホルツエネルギーだったり、f の引数は圧力でなく密度ρになっていたりとさっきと勝手が違う)
とりあえず、沸点も計算によって算出されていたことが確認できたので良かった。
IAPWS-95 式って結局何
- 水(液体)の最も良い状態方程式
- 水の熱力学的特性が広い T, p の範囲で得られる式 (温度:273.16 ~ 1273 K 圧力:0 ~ 1000 MPa の範囲)
- ヘルムホルツエネルギーの明示的な式
※ということは、ギブズエネルギーの式と等式結ぶには事前にギブズエネルギーに変換しないとだめかも
参考:Applications of the IAPWS-95 formulation in fluid inclusion and mineral-fluid phase equilibria のアブスト・イントロ内での説明が分かりやすかった。
ㅤ
まとめ:水の融点と沸点を出典付きで
沸点:99.974 ℃ (373.124 K)[b]
出どころの分からなかった水の融点・沸点の値がどこから来て、どのように得られたものなのかやっと知ることができた…!
条件を省略した文言 → 条件を明記した文言
ㅤㅤㅤ↓
「水(VSMOW)の標準気圧における沸点は、ITS-90で定義された国際セルシウス温度で 99.974℃ (と、状態方程式(IAPWS-95等) から算出されている) 」
以下、更に細かい話…
熱力学温度と国際ケルビン温度の違い
温度の定義を調べるとすぐ上に出てくる熱力学温度と、今回水の融点・沸点に用いたITS-90による国際ケルビン温度は、実は異なる。
例えばWikipedia の「ケルビン」のページに書かれている定義は熱力学温度であり、厳密には国際ケルビン温度と違う定義となる。
「温度」といえば自然科学では特に断らない限り熱力学温度の方を指していると思う。
しかしながら、熱力学温度の定義に忠実に従い温度測定を行おうとすると大掛かりな装置や手続きが必要になり、加えて再現性や安定度に問題が発生して実用的な温度測定が難しいという問題があるらしい。
そこで熱力学温度の代替として用いられているのがITS-90で定義された国際ケルビン温度である。
熱力学温度測定の誤差の範囲以内で熱力学温度に一致するため、測定の難しい熱力学温度の代わりに国際ケルビン温度を測定しても問題ない。
より詳しい情報
以上の情報は1990年国際温度目盛に関する補足情報を参考にしたもの。より詳しい内容はその補足情報を参照。国際ケルビン温度がどのように定義され、どういった装置で測定が行われるのかについても補足情報に色々と掲載されているので詳しくはそちらで。
ㅤ
(感想)
調べてみるまで水の融点・沸点の背景がこんなに奥深いなんて全く想像していませんでした…!
「標準気圧下で精度良さげな装置を使って純水の融解時・沸騰時の温度を測定する」なんて単純な話では全く無かったのですね。
融点や沸点の値が、まさか状態方程式からの計算値だったなんて…。
今回調べたことにより、"自分が何も理解していないこと"を理解できました。
本当は今回のメモ書きには不足している部分がたくさんあってもっと勉強しないといけないのですが、時間の都合上ここで一旦終了します。