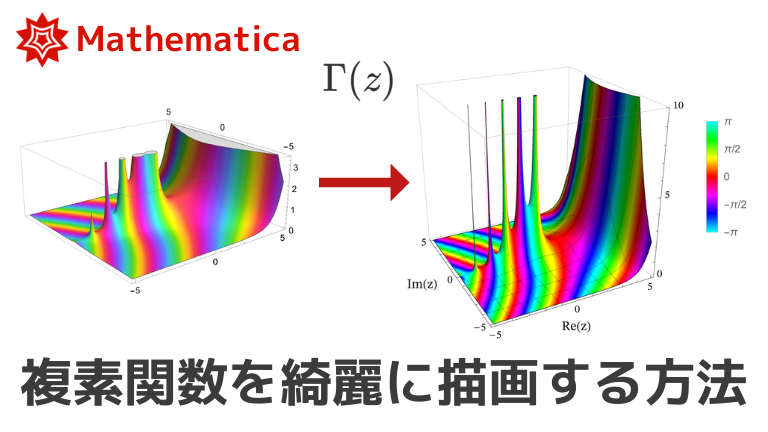
Mathematicaで複素関数のグラフを綺麗に描く最適化設定

数学ツール/アプリ(便利!)

Mathematica で複素関数の3Dグラフを描く時、標準設定だと微妙な描画になる場合があります。

例えば複素数範囲でガンマ関数を以下のコードで描画すると次のようになります。

ComplexPlot3D[Gamma[z], {z, 5}]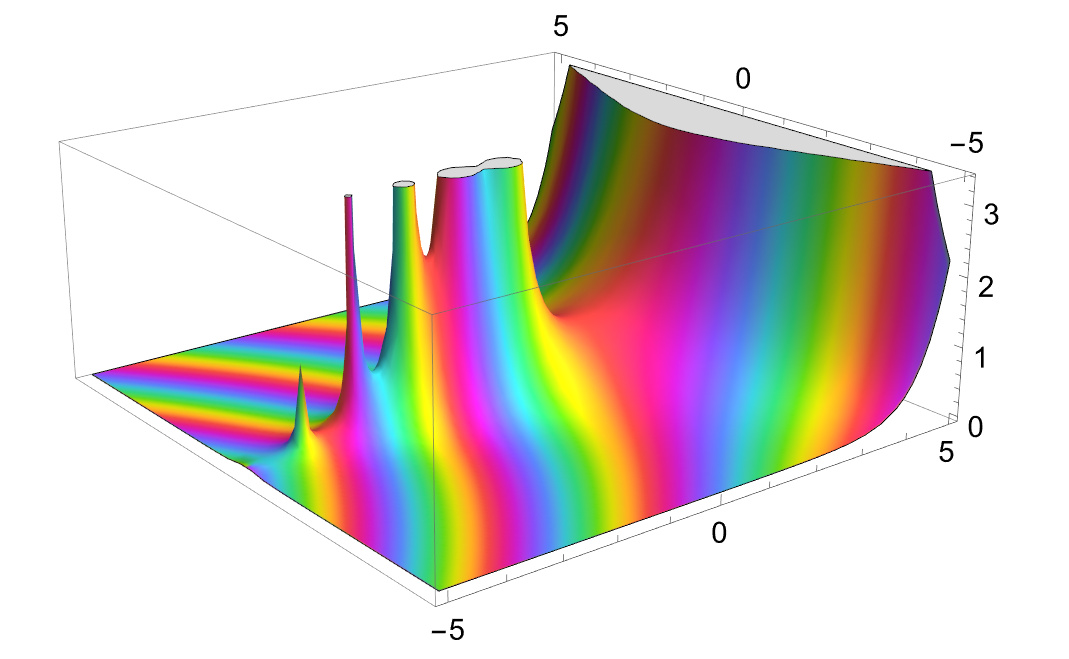

Mathematicaで描画した複素関数(ガンマ関数)の3Dプロット：標準の出力

  • 実軸/虚軸と高さ( $f(z)$ の絶対値 ) の縮尺が異なる
  • ガンマ関数の極(特に $z = -4$ の所)が精度不足でちゃんと描けていない
  • 関数グラフ表面に目盛りが無いため、$z$ が関数 $f(z)$ 上のどの位置か分かりにくい

設定を最適化することでこれらのデメリットを解消し、標準設定よりも綺麗に複素関数の3Dグラフを描画できたのでコードを共有します。

目次

複素関数の3Dグラフを綺麗に描画するコード

設定最適化後のグラフ

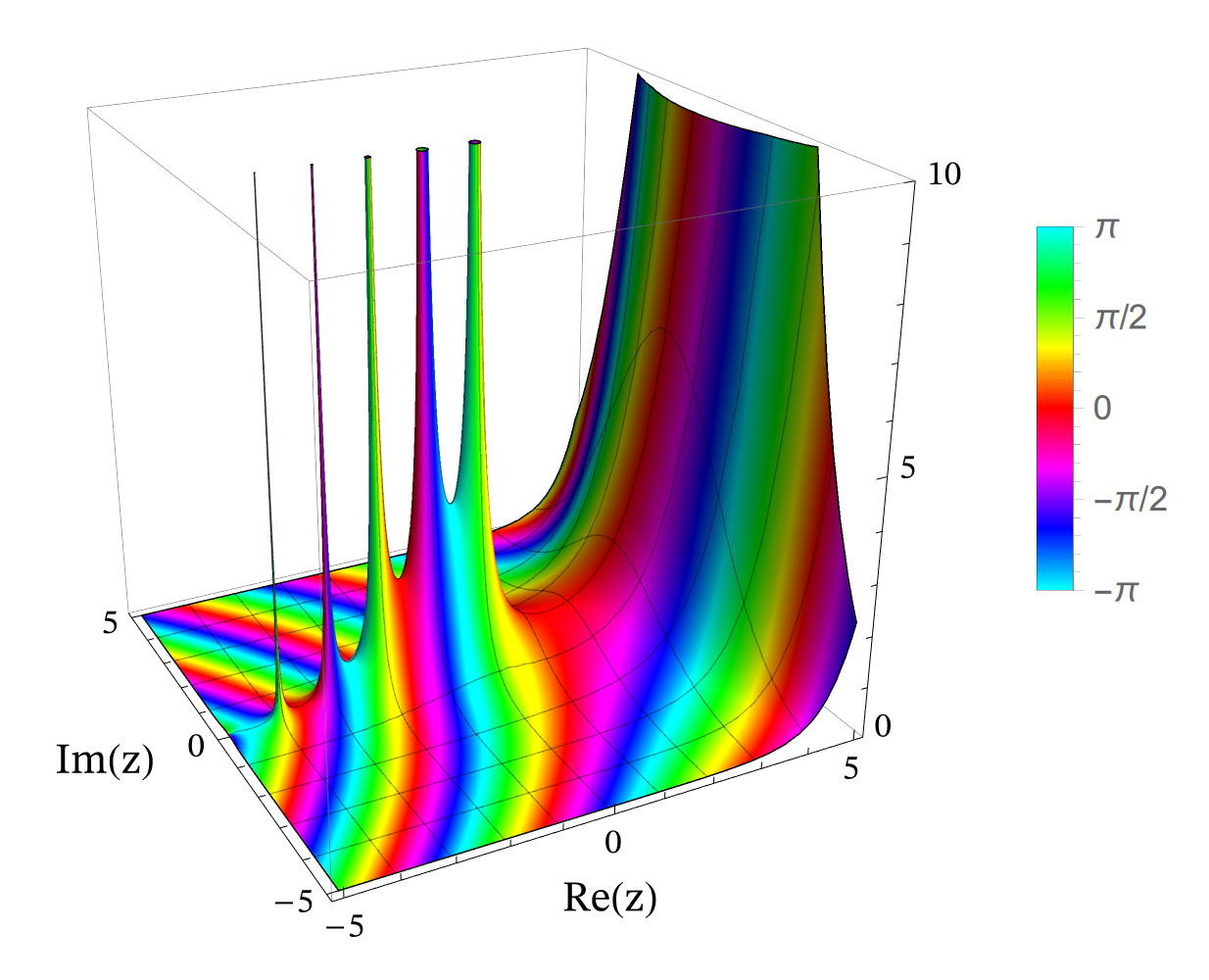
Mathematicaで描画した複素関数(ガンマ関数)の3Dプロット：最適化して綺麗にした出力

  • 関数表面に方眼線を追加して分かりやすく
  • 色と $f(z)$ の偏角の対応ラベルを右に追加
  • 色は複素関数の描画で一般によく使われるものに合わせて綺麗に
  • $z$ の実軸 Re(z) と虚軸 Im(z) のラベル追加・位置調整して見やすく
  • 実軸/虚軸と高さ( $f(z)$ の絶対値 ) の縮尺を合わせた
  • 描画精度向上で極が正確に

 

コード

$-5i-5$　～　$5i+5$ の複素数範囲でガンマ関数 Gamma[z] を描画する例です。

標準版

ComplexPlot3D[Gamma[z], {z, 5}, PlotRange -> {0, 10}, Mesh -> 9, 
  BoxRatios -> {1, 1, 1}, MaxRecursion -> 15, 
  AxesEdge -> {{-1, -1}, {-1, -1}, {1, -1}}, 
  AxesLabel -> {"Re(z)", "Im(z)"}, 
  AxesStyle -> Directive[FontSize -> 15, Black], 
  LabelStyle -> Directive[Medium], ColorFunction -> (Hue[#8 + 0.5] &), 
  PlotLegends -> BarLegend[{Hue[# + 0.5] &, {0, 1}}], 
  ClippingStyle -> None, MeshFunctions -> {Re[#1] &, Im[#1] &}, 
  MeshStyle -> Opacity[0.3]]

CC0
Pajoca (パジョカ) はこのソースコードの全ての著作権および関連する権利をCC0により放棄しています。

軸ラベル綺麗版 (要フォントインストール)

軸ラベルに STIX フォントを用いて綺麗にしたバージョンです。

STIXフォントのインストール方法はこちらのページの「STIXフォントのインストール」をご参照ください。

ComplexPlot3D[Gamma[z], {z, 5}, PlotRange -> {0, 10}, Mesh -> 9, 
 BoxRatios -> {1, 1, 1}, MaxRecursion -> 15,  
 AxesEdge -> {{-1, -1}, {-1, -1}, {1, -1}}, 
 AxesLabel -> {"Re(z)", "Im(z)"}, 
 AxesStyle -> 
  Directive[FontSize -> 15, FontFamily -> "STIX Two Math", Black], 
 LabelStyle -> Directive[Medium], ColorFunction -> (Hue[#8 + 0.5] &), 
 PlotLegends -> BarLegend[{Hue[# + 0.5] &, {0, 1}}], 
 ClippingStyle -> None, MeshFunctions -> {Re[#1] &, Im[#1] &}, 
 MeshStyle -> Opacity[0.3]]

CC0
Pajoca (パジョカ) はこのソースコードの全ての著作権および関連する権利をCC0により放棄しています。

各オプションについて

オプションのうち以下のものは都度お好みで変更してください。

  • 先頭引数：描きたい関数
  • {z, 5}：z が -5i-5 ～ +5i+5 の複素数範囲で描画
  • PlotRange -> {0, 10}：関数の絶対値が0～10の範囲で描画
  • Mesh -> 9：関数表面のメッシュ(方眼線)を9本描く
  • BoxRatios -> {1, 1, 1}：描画ボックスの幅・奥行き・高さの比
  • MaxRecursion -> 15：関数の描画計算の再帰回数。最大値の15で精度最良
  • FontFamily -> "STIX Two Math"：軸ラベルのフォント名。(フォント要インストール)

 

普段使い用に関数を簡略化

上のコードを毎回コピーして使ってもいいですが、普段使う時は「描画する関数」と「描画範囲」くらいしか変更しないと思うのでそれらを簡単に設定できるユーザー定義関数を用意しました。

 

使い方：事前準備

まず、以下のコードをコピペして実行 (Shift+Enter) します。
(※ノートブック起動のたびにこのコードを実行して関数を定義する必要があります)

complexPlot3DUser1[function_, plotRangeXY_ : 5, plotRangeZ_ : 10, 
boxRatios_ : {1, 1, 1}, maxRecursion_ : 15] :=
ComplexPlot3D[function, {z, plotRangeXY}, 
PlotRange -> {0, plotRangeZ}, Mesh -> 2*plotRangeXY - 1, 
BoxRatios -> boxRatios, MaxRecursion -> maxRecursion, 
AxesEdge -> {{-1, -1}, {-1, -1}, {1, -1}}, 
AxesLabel -> {"Re(z)", "Im(z)"}, 
AxesStyle -> Directive[FontSize -> 15, Black], 
LabelStyle -> Directive[Medium], 
ColorFunction -> (Hue[#8 + 0.5] &), 
PlotLegends -> BarLegend[{Hue[# + 0.5] &, {0, 1}}], 
ClippingStyle -> None, MeshFunctions -> {Re[#1] &, Im[#1] &}, 
MeshStyle -> Opacity[0.3]]

CC0
Pajoca (パジョカ) はこのソースコードの全ての著作権および関連する権利をCC0により放棄しています。

これでユーザー定義関数を使う準備ができました。

 

使い方：関数の描画

構文は次のとおりです。

complexPlot3DUser1[描きたい関数, z の範囲, 高さ, X軸Y軸Z軸の比率, 描画精度]

「描きたい関数」以外の引数は省略できます。(省略するとデフォルトの設定値が適用されます)

描きたい関数

描きたい複素関数を指定します。変数には z を使用してください。

例：$f(z)=z^2$ を描きたい↓

complexPlot3DUser1[z^2]

z の範囲

例えば $f(z)=z^2$ を $-4i-4$　～　$4i+4$ の複素数範囲で描きたい場合は z の範囲を 4 としてください。

complexPlot3DUser1[z^2, 4]

デフォルト値は 5 です。

高さ

関数をどの高さ ( $f(z)$ の絶対値) まで描画するかの設定値です。(デフォルト値は 10)

例えば $f(z)=z^2$ を高さ 8 まで描画したい場合は 8 を設定します。

complexPlot3DUser1[z^2, 4, 8]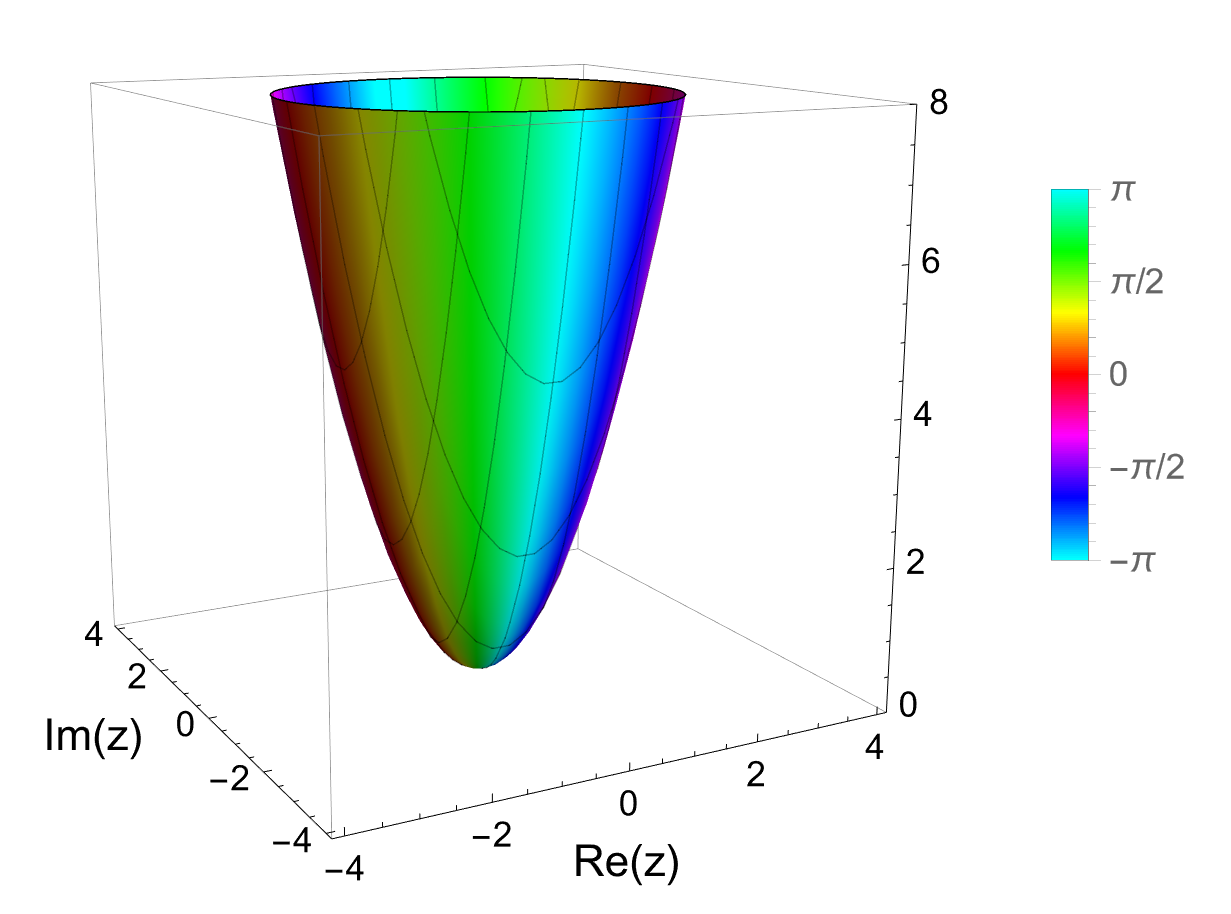

Mathematicaで描画した複素関数(z^2)の3Dプロット

X軸Y軸Z軸の比率

X軸Y軸Z軸 の比率を 1:1:2 に指定する場合なら {1, 1, 2} と指定します。

デフォルト値は {1, 1, 1} です。

描画精度

1 ～ 15 の範囲で指定でき、15が最高の描画精度です。

値を大きくするほど描画に時間がかかりますが、関数の極の描画精度が改善します。

デフォルト値は 15 です。

(例)

関数 $f(z) = z + \frac{1}{z}$ を $-10i-10$　～　$10i+10$ の複素数範囲で、高さ $20$ まで X軸Y軸Z軸 の比率 1:1:1、最高精度で描画したい場合のコードはこちらになります。

complexPlot3DUser1[z + 1/z, 10, 20, {1, 1, 1}, 15]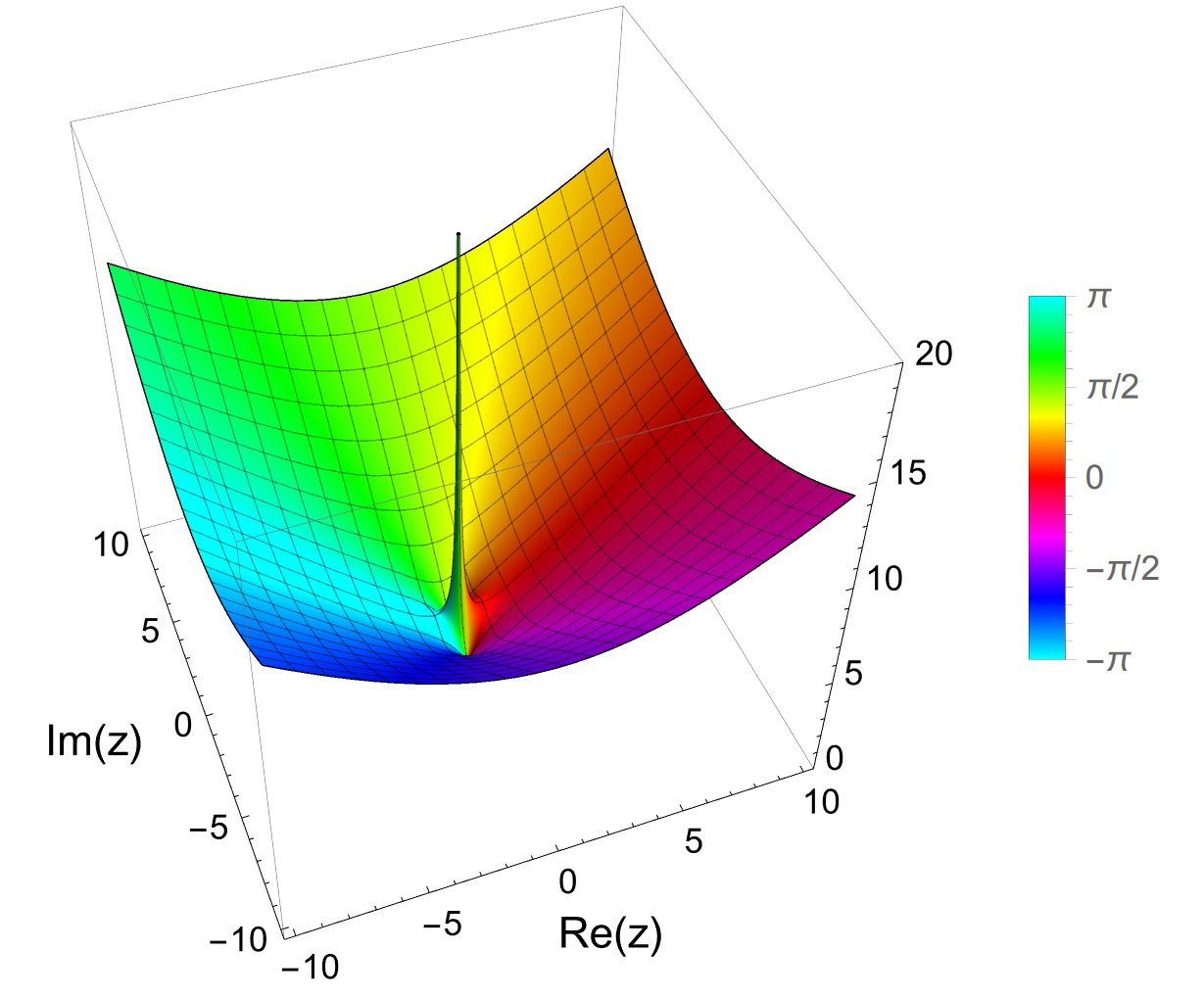

Mathematicaで描画した複素関数(z+1/z)の3Dプロット

 

参考情報

Mathematica (Wolfram 言語) で複素関数をプロットする関数 ComplexPlot3D の公式ドキュメントはこちらです。

ComplexPlot3D—Wolfram言語ドキュメント

ComplexPlot3D[f, {z, zmin, zmax}] zminと zmaxがコーナーの複素長方形上でArg…

 

今回設定しなかったオプションや、様々な描画方法についても記載されているので詳しくは上記をご参照ください。

記事化前の最新情報はこちらで先にツイートしています。サイト更新告知もこちら。

数学ツール/アプリ(便利!)の最新記事8件