スマートフォンでは、横長の数式が画面内に収まっていない場合があります
その際はタッチ操作で数式を横スクロールしてください
その際はタッチ操作で数式を横スクロールしてください
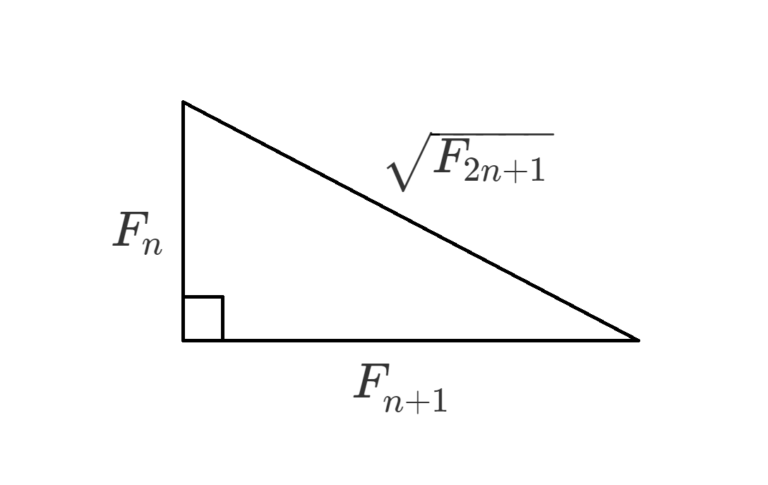
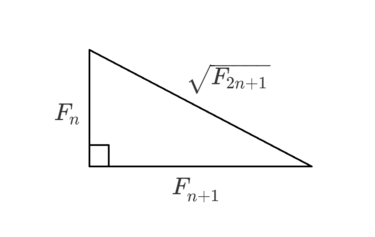
直角三角形について底辺と高さの長さが連続するフィボナッチ数である場合、斜辺の長さが別のフィボナッチ数の平方根になるという定理があります。
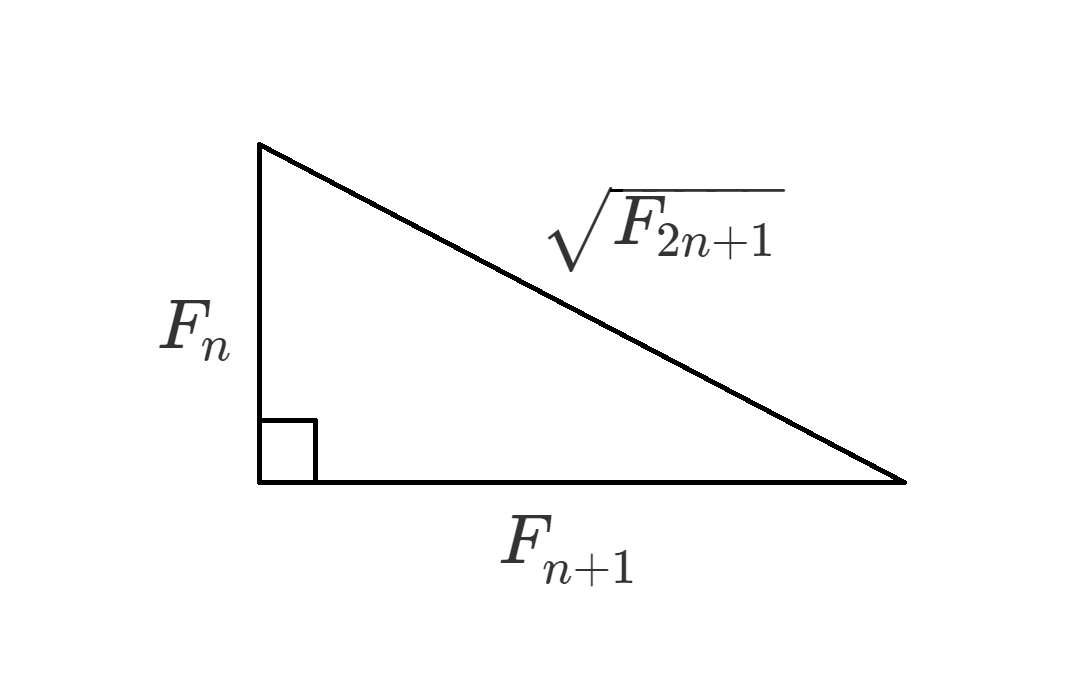
この図をどこかで見たのですが場所は忘れてしまいました😅
これが実際に成り立つことを、フィボナッチ数の加法定理を用いて証明します。
※フィボナッチ数って何? って思った方は始めにこちらを参照して下さい。
$F_n$ は $n$ 番目のフィボナッチ数です。
$(F_1=1, F_2=1, F_3=2, F_4=3, F_5=5)$
目次
定理と証明
今回証明したい三辺の関係は、三平方の定理より次の式で表せる。
\begin{equation}
F_{n}^{2}+F_{n+1}^{2} = F_{2n+1} \ \ (n \geqq 1)
\end{equation}
F_{n}^{2}+F_{n+1}^{2} = F_{2n+1} \ \ (n \geqq 1)
\end{equation}
上記定理は次のフィボナッチ数の加法定理について、$m$に$n+1$を代入することで示せる。
\begin{equation}
F_{m+n} = F_{m-1}F_{n} + F_{m}F_{n+1}
\end{equation}
F_{m+n} = F_{m-1}F_{n} + F_{m}F_{n+1}
\end{equation}
それでは、数学的帰納法を用いてフィボナッチ数の加法定理を証明する。
(証明)
ㅤ
$n=1$のとき, (2)は
\begin{eqnarray}
\mbox{(左辺)} &=& F_{m+1} \nonumber \\
\nonumber \\
\mbox{(右辺)} &=& F_{m-1}F_{1} + F_{m}F_{2} \nonumber \\
&=& F_{m-1}\cdot1 + F_{m}\cdot1 \nonumber \\
&=& F_{m-1} + F_{m} \nonumber \\
&=& F_{m+1}\nonumber
\end{eqnarray}
となり成立.
ㅤ
$n=2$のとき, (2)は
\begin{eqnarray}
\mbox{(左辺)} &=& F_{m+2} \nonumber \\
\nonumber \\
\mbox{(右辺)} &=& F_{m-1}F_{2} + F_{m}F_{3} \nonumber \\
&=& F_{m-1}\cdot1 + F_{m}\cdot2 \nonumber \\
&=& (F_{m-1} + F_{m})+ F_{m} \nonumber \\
&=& F_{m+1}+ F_{m} \nonumber \\
&=& F_{m+2} \nonumber
\end{eqnarray}
となり成立.
ㅤ
$n=k$, $n=k+1$ のとき成り立つと仮定すると, $n=k+2$ のとき, (2)は
\begin{eqnarray}
\mbox{(左辺)} &=& F_{m+k+2} \nonumber \\
\nonumber \\
\mbox{(右辺)} &=& F_{m-1}F_{k+2} + F_{m}F_{k+3} \nonumber \\
&=& F_{m-1}(F_{k+1}+F_{k}) + F_{m}(F_{k+2}+F_{k+1}) \nonumber \\
&=& (F_{m-1}F_{k} + F_{m}F_{k+1}) + (F_{m-1}F_{k+1} + F_{m}F_{k+2})\nonumber \\
&=& F_{m+k}+ F_{m+(k+1)} \nonumber \\
&=& F_{m+k+2} \nonumber
\end{eqnarray}
となり成立するので, 以上より $1$ 以上の任意の $n$ について $(2)$ 式が成り立つ.
(証明終)
ㅤ
$n=1$のとき, (2)は
\begin{eqnarray}
\mbox{(左辺)} &=& F_{m+1} \nonumber \\
\nonumber \\
\mbox{(右辺)} &=& F_{m-1}F_{1} + F_{m}F_{2} \nonumber \\
&=& F_{m-1}\cdot1 + F_{m}\cdot1 \nonumber \\
&=& F_{m-1} + F_{m} \nonumber \\
&=& F_{m+1}\nonumber
\end{eqnarray}
となり成立.
ㅤ
$n=2$のとき, (2)は
\begin{eqnarray}
\mbox{(左辺)} &=& F_{m+2} \nonumber \\
\nonumber \\
\mbox{(右辺)} &=& F_{m-1}F_{2} + F_{m}F_{3} \nonumber \\
&=& F_{m-1}\cdot1 + F_{m}\cdot2 \nonumber \\
&=& (F_{m-1} + F_{m})+ F_{m} \nonumber \\
&=& F_{m+1}+ F_{m} \nonumber \\
&=& F_{m+2} \nonumber
\end{eqnarray}
となり成立.
ㅤ
$n=k$, $n=k+1$ のとき成り立つと仮定すると, $n=k+2$ のとき, (2)は
\begin{eqnarray}
\mbox{(左辺)} &=& F_{m+k+2} \nonumber \\
\nonumber \\
\mbox{(右辺)} &=& F_{m-1}F_{k+2} + F_{m}F_{k+3} \nonumber \\
&=& F_{m-1}(F_{k+1}+F_{k}) + F_{m}(F_{k+2}+F_{k+1}) \nonumber \\
&=& (F_{m-1}F_{k} + F_{m}F_{k+1}) + (F_{m-1}F_{k+1} + F_{m}F_{k+2})\nonumber \\
&=& F_{m+k}+ F_{m+(k+1)} \nonumber \\
&=& F_{m+k+2} \nonumber
\end{eqnarray}
となり成立するので, 以上より $1$ 以上の任意の $n$ について $(2)$ 式が成り立つ.
(証明終)
ㅤ