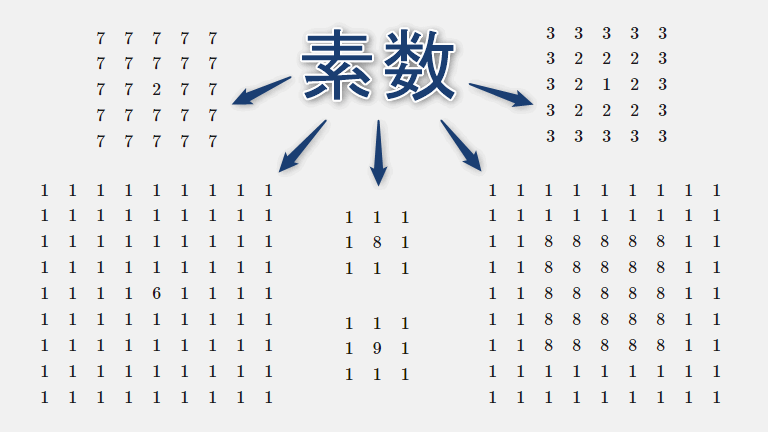
その際はタッチ操作で数式を横スクロールしてください
「見て楽しい」観賞用の素数ギャラリー。
今回は、各桁の数字を正方形になるように並べると超綺麗に見えるような素数を集めました。
全て回文素数ですが、ただの回文素数よりも(見た目の)対称性が高くてもっと綺麗に見えます!
3×3 正方形 (9ケタの素数)
111181111 と 111191111 のペア
1&1&1\\
1&8&1\\
1&1&1\\
\end{matrix}
1&1&1\\
1&9&1\\
1&1&1\\
\end{matrix}
そして $181$ と $191$ も素数!
777767777
7&7&7\\
7&6&7\\
7&7&7\\
\end{matrix}
9ケタの素数で、以下のように対称的な正方形に並べられるものは上記の3通りのみ!
\begin{matrix}
b&b&b\\
b&a&b\\
b&b&b\\
\end{matrix}
5×5 正方形 (25ケタの素数)
7777777777772777777777777
7&7&7&7&7\\
7&7&7&7&7\\
7&7&2&7&7\\
7&7&7&7&7\\
7&7&7&7&7\\
\end{matrix}
25ケタの素数で、正方形の中心の数字以外が全部同じになるように並べられるものは $7777777777772777777777777$ のみ!
1111118881188811888111111
1&1&1&1&1\\
1&8&8&8&1\\
1&8&8&8&1\\
1&8&8&8&1\\
1&1&1&1&1\\
\end{matrix}
8でできた正方形の外周を1が囲む。このタイプも25ケタの素数では $1111118881188811888111111$ のみ!
正方形の辺と中心の数字が等しいパターン
3&3&3&3&3\\
3&1&1&1&3\\
3&1&3&1&3\\
3&1&1&1&3\\
3&3&3&3&3\\
\end{matrix}
3&3&3&3&3\\
3&5&5&5&3\\
3&5&3&5&3\\
3&5&5&5&3\\
3&3&3&3&3\\
\end{matrix}
1&1&1&1&1\\
1&6&6&6&1\\
1&6&1&6&1\\
1&6&6&6&1\\
1&1&1&1&1\\
\end{matrix}
7&7&7&7&7\\
7&3&3&3&7\\
7&3&7&3&7\\
7&3&3&3&7\\
7&7&7&7&7\\
\end{matrix}
特に右上。$353$ と $35353$ も素数!!
(左上。$313$ は素数だけど $31313=173\times 181$ は素数でない)
25ケタの素数で、正方形に並べたときに辺の数字と中心の数字が等しく、残りの数字が全て一致するようなパターンは上記の
$1111116661161611666111111,$
$3333331113313133111333333,$
$3333335553353533555333333,$
$7777773337737377333777777$ の4個のみ!
3種類の数字からなるパターン
3333332223321233222333333
3&3&3&3&3\\
3&2&2&2&3\\
3&2&1&2&3\\
3&2&2&2&3\\
3&3&3&3&3\\
\end{matrix}
外側から内側へ 3→2→1 と ステップダウンする綺麗な形!
(1ずつステップアップorダウンするパターンはこれのみ!)
9999994449946499444999999 と 9999995559956599555999999のペア
9&9&9&9&9\\
9&4&4&4&9\\
9&4&6&4&9\\
9&4&4&4&9\\
9&9&9&9&9\\
\end{matrix}
9&9&9&9&9\\
9&5&5&5&9\\
9&5&6&5&9\\
9&5&5&5&9\\
9&9&9&9&9\\
\end{matrix}
辺と中心の数字は共通。内部が $4$ と $5$ で $1$ 違いのペア。
1111118881182811888111111 と 1111119991193911999111111 のペア
1&1&1&1&1\\
1&8&8&8&1\\
1&8&2&8&1\\
1&8&8&8&1\\
1&1&1&1&1\\
\end{matrix}
1&1&1&1&1\\
1&9&9&9&1\\
1&9&3&9&1\\
1&9&9&9&1\\
1&1&1&1&1\\
\end{matrix}
辺が $1$ で共通、左の素数の内部の数字 $888828888$ を1ずつ上げると右の素数の内部 $999939999$ に!
以上のような、3種類の数字からなるパターンは(上記のものも含め)全部で $16$ 個。(一覧は後述。)
7×7 正方形 (49ケタの素数)
3-2-1正方形素数の進化版
3333333322222332111233211123321112332222233333333
\begin{matrix}
3&3&3&3&3\\
3&2&2&2&3\\
3&2&1&2&3\\
3&2&2&2&3\\
3&3&3&3&3\\
\end{matrix}
\begin{matrix}
3&3&3&3&3&3&3\\
3&2&2&2&2&2&3\\
3&2&1&1&1&2&3\\
3&2&1&1&1&2&3\\
3&2&1&1&1&2&3\\
3&2&2&2&2&2&3\\
3&3&3&3&3&3&3\\
\end{matrix}
5×5正方形の時にあった「外側から内側へ 3→2→1 と ステップダウンする形」がなんと7×7でも!! (超綺麗!)
2種類の数字のみ
1111111144444114111411414141141114114444411111111
1&1&1&1&1&1&1\\
1&4&4&4&4&4&1\\
1&4&1&1&1&4&1\\
1&4&1&4&1&4&1\\
1&4&1&1&1&4&1\\
1&4&4&4&4&4&1\\
1&1&1&1&1&1&1\\
\end{matrix}
7777777733333773777377373737737773773333377777777
7&7&7&7&7&7&7\\
7&3&3&3&3&3&7\\
7&3&7&7&7&3&7\\
7&3&7&3&7&3&7\\
7&3&7&7&7&3&7\\
7&3&3&3&3&3&7\\
7&7&7&7&7&7&7\\
\end{matrix}
7777777788888778777877877787787778778888877777777
7&7&7&7&7&7&7\\
7&8&8&8&8&8&7\\
7&8&7&7&7&8&7\\
7&8&7&7&7&8&7\\
7&8&7&7&7&8&7\\
7&8&8&8&8&8&7\\
7&7&7&7&7&7&7\\
\end{matrix}
49ケタの素数で、2種類の数字のみから成る対称な正方形の形に並べることができるのは上記の3数のみ!!
中心の数字だけが異なるペア
1&1&1&1&1&1&1\\
1&4&4&4&4&4&1\\
1&4&1&1&1&4&1\\
1&4&1&4&1&4&1\\
1&4&1&1&1&4&1\\
1&4&4&4&4&4&1\\
1&1&1&1&1&1&1\\
\end{matrix}
1&1&1&1&1&1&1\\
1&4&4&4&4&4&1\\
1&4&1&1&1&4&1\\
1&4&1&5&1&4&1\\
1&4&1&1&1&4&1\\
1&4&4&4&4&4&1\\
1&1&1&1&1&1&1\\
\end{matrix}
$1111111144444114111411414141141114114444411111111,$
$1111111144444114111411415141141114114444411111111$
3&3&3&3&3&3&3\\
3&0&0&0&0&0&3\\
3&0&3&3&3&0&3\\
3&0&3&2&3&0&3\\
3&0&3&3&3&0&3\\
3&0&0&0&0&0&3\\
3&3&3&3&3&3&3\\
\end{matrix}
3&3&3&3&3&3&3\\
3&0&0&0&0&0&3\\
3&0&3&3&3&0&3\\
3&0&3&8&3&0&3\\
3&0&3&3&3&0&3\\
3&0&0&0&0&0&3\\
3&3&3&3&3&3&3\\
\end{matrix}
$3333333300000330333033032303303330330000033333333,$
$3333333300000330333033038303303330330000033333333$
7&7&7&7&7&7&7\\
7&3&3&3&3&3&7\\
7&3&9&9&9&3&7\\
7&3&9&5&9&3&7\\
7&3&9&9&9&3&7\\
7&3&3&3&3&3&7\\
7&7&7&7&7&7&7\\
\end{matrix}
7&7&7&7&7&7&7\\
7&3&3&3&3&3&7\\
7&3&9&9&9&3&7\\
7&3&9&7&9&3&7\\
7&3&9&9&9&3&7\\
7&3&3&3&3&3&7\\
7&7&7&7&7&7&7\\
\end{matrix}
$7777777733333773999377395937739993773333377777777,$
$7777777733333773999377397937739993773333377777777$
9&9&9&9&9&9&9\\
9&4&4&4&4&4&9\\
9&4&0&0&0&4&9\\
9&4&0&1&0&4&9\\
9&4&0&0&0&4&9\\
9&4&4&4&4&4&9\\
9&9&9&9&9&9&9\\
\end{matrix}
9&9&9&9&9&9&9\\
9&4&4&4&4&4&9\\
9&4&0&0&0&4&9\\
9&4&0&4&0&4&9\\
9&4&0&0&0&4&9\\
9&4&4&4&4&4&9\\
9&9&9&9&9&9&9\\
\end{matrix}
$9999999944444994000499401049940004994444499999999,$
$9999999944444994000499404049940004994444499999999$
9×9 正方形 (81ケタの素数)
※全探索したけど、結果はまとめ途中。条件を満たす素数がそれだけかは未チェック。
ラッキー7の織りなす奇跡
先ほど取り上げた7×7 正方形素数をもう一度。
7&7&7&7&7&7&7\\
7&8&8&8&8&8&7\\
7&8&7&7&7&8&7\\
7&8&7&7&7&8&7\\
7&8&7&7&7&8&7\\
7&8&8&8&8&8&7\\
7&7&7&7&7&7&7\\
\end{matrix}
この素数の正方形の外周に、更に7を追加してできる 9×9 正方形もなんと素数!!!!!!!
7&7&7&7&7&7&7&7&7\\
7&7&7&7&7&7&7&7&7\\
7&7&8&8&8&8&8&7&7\\
7&7&8&7&7&7&8&7&7\\
7&7&8&7&7&7&8&7&7\\
7&7&8&7&7&7&8&7&7\\
7&7&8&8&8&8&8&7&7\\
7&7&7&7&7&7&7&7&7\\
7&7&7&7&7&7&7&7&7\\
\end{matrix}
偶然でもこれは凄い…!!!
恐るべき
7777777788888778777877877787787778778888877777777,
777777777777777777778888877778777877778777877778777877778888877777777777777777777
ペア…。
1の海の中心に鎮座する6
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&1&1&6&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
\end{matrix}
中心以外の全数字が一致するパターンは多分これだけ。
111111111111111111111111111111111111111161111111111111111111111111111111111111111
1の海に浮かぶ8島・9島ペア
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&8&8&8&8&8&1&1\\
1&1&8&8&8&8&8&1&1\\
1&1&8&8&8&8&8&1&1\\
1&1&8&8&8&8&8&1&1\\
1&1&8&8&8&8&8&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
\end{matrix}
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&9&9&9&9&9&1&1\\
1&1&9&9&9&9&9&1&1\\
1&1&9&9&9&9&9&1&1\\
1&1&9&9&9&9&9&1&1\\
1&1&9&9&9&9&9&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
\end{matrix}
1の海の上に、5×5サイズの「8の島」と「9の島」が浮かぶ
111111111111111111118888811118888811118888811118888811118888811111111111111111111,
111111111111111111119999911119999911119999911119999911119999911111111111111111111
2種類の数字のみ
1&1&1&1&1&1&1&1&1\\
1&9&9&9&9&9&9&9&1\\
1&9&9&9&9&9&9&9&1\\
1&9&9&1&1&1&9&9&1\\
1&9&9&1&1&1&9&9&1\\
1&9&9&1&1&1&9&9&1\\
1&9&9&9&9&9&9&9&1\\
1&9&9&9&9&9&9&9&1\\
1&1&1&1&1&1&1&1&1\\
\end{matrix}
7&7&7&7&7&7&7&7&7\\
7&7&7&7&7&7&7&7&7\\
7&7&8&8&8&8&8&7&7\\
7&7&8&7&7&7&8&7&7\\
7&7&8&7&7&7&8&7&7\\
7&7&8&7&7&7&8&7&7\\
7&7&8&8&8&8&8&7&7\\
7&7&7&7&7&7&7&7&7\\
7&7&7&7&7&7&7&7&7\\
\end{matrix}
9&9&9&9&9&9&9&9&9\\
9&9&9&9&9&9&9&9&9\\
9&9&5&5&5&5&5&9&9\\
9&9&5&5&5&5&5&9&9\\
9&9&5&5&5&5&5&9&9\\
9&9&5&5&5&5&5&9&9\\
9&9&5&5&5&5&5&9&9\\
9&9&9&9&9&9&9&9&9\\
9&9&9&9&9&9&9&9&9\\
\end{matrix}
111111111199999991199999991199111991199111991199111991199999991199999991111111111,
777777777777777777778888877778777877778777877778777877778888877777777777777777777,
999999999999999999995555599995555599995555599995555599995555599999999999999999999
各桁が素数な正方形素数
3&3&3&3&3&3&3&3&3\\
3&2&2&2&2&2&2&2&3\\
3&2&5&5&5&5&5&2&3\\
3&2&5&7&7&7&5&2&3\\
3&2&5&7&7&7&5&2&3\\
3&2&5&7&7&7&5&2&3\\
3&2&5&5&5&5&5&2&3\\
3&2&2&2&2&2&2&2&3\\
3&3&3&3&3&3&3&3&3\\
\end{matrix}
各桁が1桁の素数 $2,3,5,7$ のみからなる、見た目の素数感が幸せな素数正方形!
しかも中央の行の $325777523$ も素数!
ちなみに端の隣の行 $322222223$ も素数!
$23, 223, 523, 7523$ も素数!各桁が素数な素数がいっぱい!
(例外もあるから注意)
(なお、中心の1文字 $7$ を $9$ に変えても素数)
333333333322222223325555523325777523325777523325777523325555523322222223333333333,
333333333322222223325555523325777523325797523325777523325555523322222223333333333
中心の数が隣り合うペア
中心が 5, 6 のペア
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&4&4&4&4&4&1&1\\
1&1&4&1&1&1&4&1&1\\
1&1&4&1&5&1&4&1&1\\
1&1&4&1&1&1&4&1&1\\
1&1&4&4&4&4&4&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
\end{matrix}
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&4&4&4&4&4&1&1\\
1&1&4&1&1&1&4&1&1\\
1&1&4&1&6&1&4&1&1\\
1&1&4&1&1&1&4&1&1\\
1&1&4&4&4&4&4&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
\end{matrix}
111111111111111111114444411114111411114151411114111411114444411111111111111111111,
111111111111111111114444411114111411114161411114111411114444411111111111111111111
中心が 4, 5 のペア
1&1&1&1&1&1&1&1&1\\
1&5&5&5&5&5&5&5&1\\
1&5&5&5&5&5&5&5&1\\
1&5&5&4&4&4&5&5&1\\
1&5&5&4&4&4&5&5&1\\
1&5&5&4&4&4&5&5&1\\
1&5&5&5&5&5&5&5&1\\
1&5&5&5&5&5&5&5&1\\
1&1&1&1&1&1&1&1&1\\
\end{matrix}
1&1&1&1&1&1&1&1&1\\
1&5&5&5&5&5&5&5&1\\
1&5&5&5&5&5&5&5&1\\
1&5&5&4&4&4&5&5&1\\
1&5&5&4&5&4&5&5&1\\
1&5&5&4&4&4&5&5&1\\
1&5&5&5&5&5&5&5&1\\
1&5&5&5&5&5&5&5&1\\
1&1&1&1&1&1&1&1&1\\
\end{matrix}
111111111155555551155555551155444551155444551155444551155555551155555551111111111,
111111111155555551155555551155444551155454551155444551155555551155555551111111111
1 → 3 → 5 ステップアップ
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&3&3&3&3&3&1&1\\
1&1&3&5&5&5&3&1&1\\
1&1&3&5&5&5&3&1&1\\
1&1&3&5&5&5&3&1&1\\
1&1&3&3&3&3&3&1&1\\
1&1&1&1&1&1&1&1&1\\
1&1&1&1&1&1&1&1&1\\
\end{matrix}
111111111111111111113333311113555311113555311113555311113333311111111111111111111
3 → 5 → 7 ステップアップ
3&3&3&3&3&3&3&3&3\\
3&5&5&5&5&5&5&5&3\\
3&5&5&5&5&5&5&5&3\\
3&5&5&5&5&5&5&5&3\\
3&5&5&5&7&5&5&5&3\\
3&5&5&5&5&5&5&5&3\\
3&5&5&5&5&5&5&5&3\\
3&5&5&5&5&5&5&5&3\\
3&3&3&3&3&3&3&3&3\\
\end{matrix}
333333333355555553355555553355555553355575553355555553355555553355555553333333333
9 → 7 → 5 ステップダウン
9&9&9&9&9&9&9&9&9\\
9&7&7&7&7&7&7&7&9\\
9&7&7&7&7&7&7&7&9\\
9&7&7&5&5&5&7&7&9\\
9&7&7&5&5&5&7&7&9\\
9&7&7&5&5&5&7&7&9\\
9&7&7&7&7&7&7&7&9\\
9&7&7&7&7&7&7&7&9\\
9&9&9&9&9&9&9&9&9\\
\end{matrix}
999999999977777779977777779977555779977555779977555779977777779977777779999999999
3 → 2 → 1 →3
3&3&3&3&3&3&3&3&3\\
3&2&2&2&2&2&2&2&3\\
3&2&2&2&2&2&2&2&3\\
3&2&2&1&1&1&2&2&3\\
3&2&2&1&3&1&2&2&3\\
3&2&2&1&1&1&2&2&3\\
3&2&2&2&2&2&2&2&3\\
3&2&2&2&2&2&2&2&3\\
3&3&3&3&3&3&3&3&3\\
\end{matrix}
いやそこは空気読んで中心も $1$ にしようよ…。
333333333322222223322222223322111223322131223322111223322222223322222223333333333
検証用コード・データ
↑のギャラリーには載せなかった対称素数全探索リストもこちらにあります。
素数判定/素因数分解
上記の素数たちが本当に素数かどうか確かめるために、数十桁~百桁以上の数の素数判定・素因数分解ができるこちらのサイトを利用してみてください。
素因数分解サイトの多くが入力できる桁数に制限を設けていますが、こちらのツールは入力に小さな制限が無く便利です!
数十桁でも素数判定なら非常に高速に行ってくれます。(ただし素因数分解は桁数に応じて飛躍的に計算時間がかかります。)
(ちなみに計算自体はサイト側のサーバーではなく上記サイトを表示している端末側で行われています。計算速度は端末に依存するかも。)
探索用コード
Mathematica (科学計算ソフト) で以下の Wolfram言語を入力し実行することで、私が得た結果と同じものを得ることができます。
結果を検証したい場合や、コードを変えて別の素数を探索する場合にお使いください。
仕様
以下の見た目の素数のみを探索するコードです。
\begin{matrix}
e&e&e&e&e&e&e&e&e\\
e&d&d&d&d&d&d&d&e\\
e&d&c&c&c&c&c&d&e\\
e&d&c&b&b&b&c&d&e\\
e&d&c&b&a&b&c&d&e\\
e&d&c&b&b&b&c&d&e\\
e&d&c&c&c&c&c&d&e\\
e&d&d&d&d&d&d&d&e\\
e&e&e&e&e&e&e&e&e\\
\end{matrix}
中心から外側に向かうようにアルファベットを割り振っています。
同じ数字が正方形の辺or内部をぐるりと一周するような見た目のものを探索しましたが、正方形に並べて対称に見えるパターンはこれ以外にも存在します。
(1行が同じ数字ではなく、2種の数字が交互に並んだ上で正方形に並べて対称になるものなど。)
そのような素数は探索できていないので、必要に応じて以下のコードを改変して探してみてください。
※コードは特に計算時間短縮のための工夫をしていません。必要に応じて変更してください。
3×3 正方形素数全探索コード
Solve[10^8*b+10^7*b+10^6*b+10^5*b+10^4*a+10^3*b+10^2*b+10*b+b==p&&0<= a<=9&&1<=b<=9&&Element[p,Primes],{b,a,p},Integers]5×5 正方形素数全探索コード
Solve[
10^24*c+10^23*c+10^22*c+10^21*c+10^20*c
+10^19*c+10^18*b+10^17*b+10^16*b+10^15*c+10^14*c+10^13*b+10^12*a+10^11*b+10^10*c
+10^9*c+10^8*b+10^7*b+10^6*b+10^5*c+10^4*c+10^3*c+10^2*c+10*c+c==p
&&(c==1||c==3||c==7||c==9)
&&(b==0||b==1||b==2||b==3||b==4||b==5||b==6||b==7||b==8||b==9)
&&(a==0||a==1||a==2||a==3||a==4||a==5||a==6||a==7||a==8||a==9)
&&Element[p,Primes],{c,b,a,p},Integers]※不等式で 0<= b<=9 のように指定しして計算すると(整数範囲で探索するよう指定しているにも関わらず)なぜか探索に時間がかかります。
明示的に、辺 $c$ は 1, 3, 7, 9 のいずれか、 $b$ と $a$ は 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 の10択のいずれかであることを条件にして探索すると、(不等式を指定した場合と表している内容は同じであるにもかかわらず) 探索が高速になります。
Mathematica (Wolfram言語) のこういう仕様をよく分かっていない😅
7×7 正方形素数全探索コード
Solve[10^48*d+10^47*d+10^46*d+10^45*d+10^44*d+10^43*d+10^42*d+10^41*d+10^40*c+10^39*c+10^38*c+10^37*c+10^36*c+10^35*d+10^34*d+10^33*c+10^32*b+10^31*b+10^30*b+10^29*c+10^28*d+10^27*d+10^26*c+10^25*b+10^24*a+10^23*b+10^22*c+10^21*d+10^20*d+10^19*c+10^18*b+10^17*b+10^16*b+10^15*c+10^14*d+10^13*d+10^12*c+10^11*c+10^10*c+10^9*c+10^8*c+10^7*d+10^6*d+10^5*d+10^4*d+10^3*d+10^2*d+10*d+d==p&&( d==1 || d==3 || d==7||d==9)&&( c==0|| c==1 ||c==2||c==3||c==4||c==5||c==6||c==7||c==8||c==9)&&( b==0|| b==1 ||b==2||b==3||b==4||b==5||b==6||b==7||b==8||b==9)&&( a==0|| a==1 || a==2|| a==3|| a==4|| a==5|| a==6|| a==7|| a==8|| a==9)&&Element[p,Primes],{d,c,b,a,p},Integers](ごめんなさい。整形していないので1行コードになっていてい見づらいです。)
実行に要した時間はこちらの環境で150秒ぐらいです。
9×9 正方形素数全探索コード
Solve[10^80*e+10^79*e+10^78*e+10^77*e+10^76*e+10^75*e+10^74*e+10^73*e+10^72*e+10^71*e+10^70*d+10^69*d+10^68*d+10^67*d+10^66*d+10^65*d+10^64*d+10^63*e+10^62*e+10^61*d+10^60*c+10^59*c+10^58*c+10^57*c+10^56*c+10^55*d+10^54*e+10^53*e+10^52*d+10^51*c+10^50*b+10^49*b+10^48*b+10^47*c+10^46*d+10^45*e+10^44*e+10^43*d+10^42*c+10^41*b+10^40*a+10^39*b+10^38*c+10^37*d+10^36*e+10^35*e+10^34*d+10^33*c+10^32*b+10^31*b+10^30*b+10^29*c+10^28*d+10^27*e+10^26*e+10^25*d+10^24*c+10^23*c+10^22*c+10^21*c+10^20*c+10^19*d+10^18*e+10^17*e+10^16*d+10^15*d+10^14*d+10^13*d+10^12*d+10^11*d+10^10*d+10^9*e+10^8*e+10^7*e+10^6*e+10^5*e+10^4*e+10^3*e+10^2*e+10*e+e==p&&( e==1 || e==3 || e==7||e==9)&&( d==0|| d==1 ||d==2||d==3||d==4||d==5||d==6||d==7||d==8||d==9)&&( c==0|| c==1 ||c==2||c==3||c==4||c==5||c==6||c==7||c==8||c==9)&&( b==0|| b==1 ||b==2||b==3||b==4||b==5||b==6||b==7||b==8||b==9)&&( a==0|| a==1 || a==2|| a==3|| a==4|| a==5|| a==6|| a==7|| a==8|| a==9)&&Element[p,Primes],{e,d,c,b,a,p},Integers]実行に要した時間を計り忘れてしまいましたが、寝て起きたら探索が完了していたので6時間未満かな。
素数全探索リスト
全探索した結果をまとめたテキストファイルはこちらです。(Mathematicaでの出力結果をちょっとだけ整形したもの)
※中心から外側に向かうようにアルファベットを割り振っています。
※ p は該当する素数です。
| サイズ | 個数 | ファイル |
| 3×3 正方形素数 | 3 | 3x3-square-congruent-prime-list.txt |
| 5×5 正方形素数 | 22 | 5x5-square-congruent-prime-list.txt |
| 7×7 正方形素数 | 74 | 7x7-square-congruent-prime-list.txt |
| 9×9 正方形素数 | 588 | 9x9-square-congruent-prime-list.txt |
見て楽しい素数についての感想
今回取り上げた正方形素数は、10進法表記で正方形に並べるとたまたま見た目が綺麗になるというだけのあまり意義深くない素数たちです。
その分、何も深いことを考えずに気楽に見て楽しめます!
このような素数を探すときも、まるで宝探しをしているようなワクワク感を味わえるので幸せです。
今回は工夫しませんでしたが、探索のアルゴリズムを色々考えて高速化すると良いトレーニングになるかもしれません。
(そのうちMathematica(Wolfram言語)以外の、皆が無料で容易に実行できる言語のソースコードも掲載しようと思います。)