素数・整数ニュース【2023】

今年(2023)に目にした素数・整数関連のニュースを簡潔に一覧にしました。

素数・整数のトピックは適当に不定期で確認していただけなので、内容スカスカです…。(ごめんなさい)

(単に私が覚えているものをピックアップしただけなので重要な整数ニュースを多数見逃していると思います…。)(来年からちゃんとメモする予定)

※私でも簡単に(表面を)理解できるような内容のものばかりで、専門的なトピックが含まれていません。
ニュースと言っておきながらジャーナルにはほぼ目を通していないので内容が「特定の形をした素数発見」みたいなものに偏っています…。

4月

9番目のデデキント数が発見される

(2023/4/3・4/6)

今年の4月に、9番目のデデキント数が発見(計算)されました。(42桁)

8番目のデデキント数 $56130437228687557907788$ が発見されたのが 1991年(発見者: Wiedemann)なので、32年ぶりにデデキント数が発見されたことになります。

今回の9番目のデデキント数は ① Christian Jäkel と、② Lennart Van Hirtum らのグループ の二者によって4月上旬のほぼ同時期にプレプリントにて公開されました。(タイミングの一致が凄い偶然)

計算の鍵はデデキント数を求める効率的なアルゴリズムの開発と、高性能なGPUの利用にあるようです。

(① Christian Jäkel では、Nvidia A100 GPU が計算に用いられていました。(※論文参照) )

デデキント数について

そもそもデデキント数が何か気になる方は以下のページをご覧ください。

デデキント数の説明

デデキント数の概要 (メモ)

[usemath] [sumaho] 今年(2023)、9番目のデデキント数が発見されて32年ぶりにデデキント数のメンバーが更新されたという情報を耳にしてデデキント数について気になったので、学習メモを残しました。 (注意は払い[…]

Wikipedia を読んでもよく分からなかったという方もぜひ。(上記ページの説明ももし分かりにくかったらごめんなさい…)

ブール関数の例を挙げながら具体的に $D(1)=3$ や $D(2)=6$ を求めているので、イメージが湧くと思います。

参考情報源

9番目のデデキント数が報告された2つのプレプリントです。
(論文PDFは、ページ右側にある「Download PDF」リンクから閲覧できます)

① Jäkel, Christian. "A computation of the ninth Dedekind Number." arXiv preprint arXiv:2304.00895 (2023).
https://arxiv.org/abs/2304.00895

② Van Hirtum, Lennart, et al. "A computation of D (9) using FPGA Supercomputing." arXiv preprint arXiv:2304.03039 (2023).
https://arxiv.org/abs/2304.03039

5月

1111…1111 (86453桁) が素数であると証明される

(2023/5/16)

86453 個の「1」が並んだ整数 $1111 \dots 1111$ の素数性が証明されました。

このように(10進法で) $1$ を $n$ 個並べた数はレピュニット(Repunit)と呼ばれ、$R_n$ や $R(n)$ と表記されます。

(例)：$R(2) = 11, \ R(19) = 1111111111111111111$ はレピュニット素数。

素数性が証明されたレピュニット数は $R(2), R(19), R(23), R(317), R(1031), R(49081)$ の6個だけであったため、今回の $R(86453)$ が7番目のレピュニット素数となり、既知のレピュニット素数としては最大の大きさになります。

元々 $R(86453)$ は 2000/10/26 に Lew Baxter により確率的素数として発見されていましたが、実際に素数であると証明されるまでに約22年半かかった形です。

素数性の証明には ECPP(elliptic curve primality proving：楕円曲線素数判定法) が用いられ、確率的素数だった $R(86453)$ が実際に素数であることが検証されました。

同時に、ECPPで素数性が証明された素数としては最大記録になりました。

(リンク：ECPPで素数性が証明された素数TOP20)

参考情報源

オンライン整数列大辞典(OEIS)：レピュニット素数
A004023 (Indices of prime repunits: numbers n such that 11...111 (with n 1's) = (10^n - 1)/9 is prime.)

素数レコードサイト上での当該素数ページ
PrimePage：R(86453)

レピュニットについての説明と現在の発見状況
PrimePage Primes: Repunit

素数の等差数列の最長記録タイが発見される

(2023/5/26)

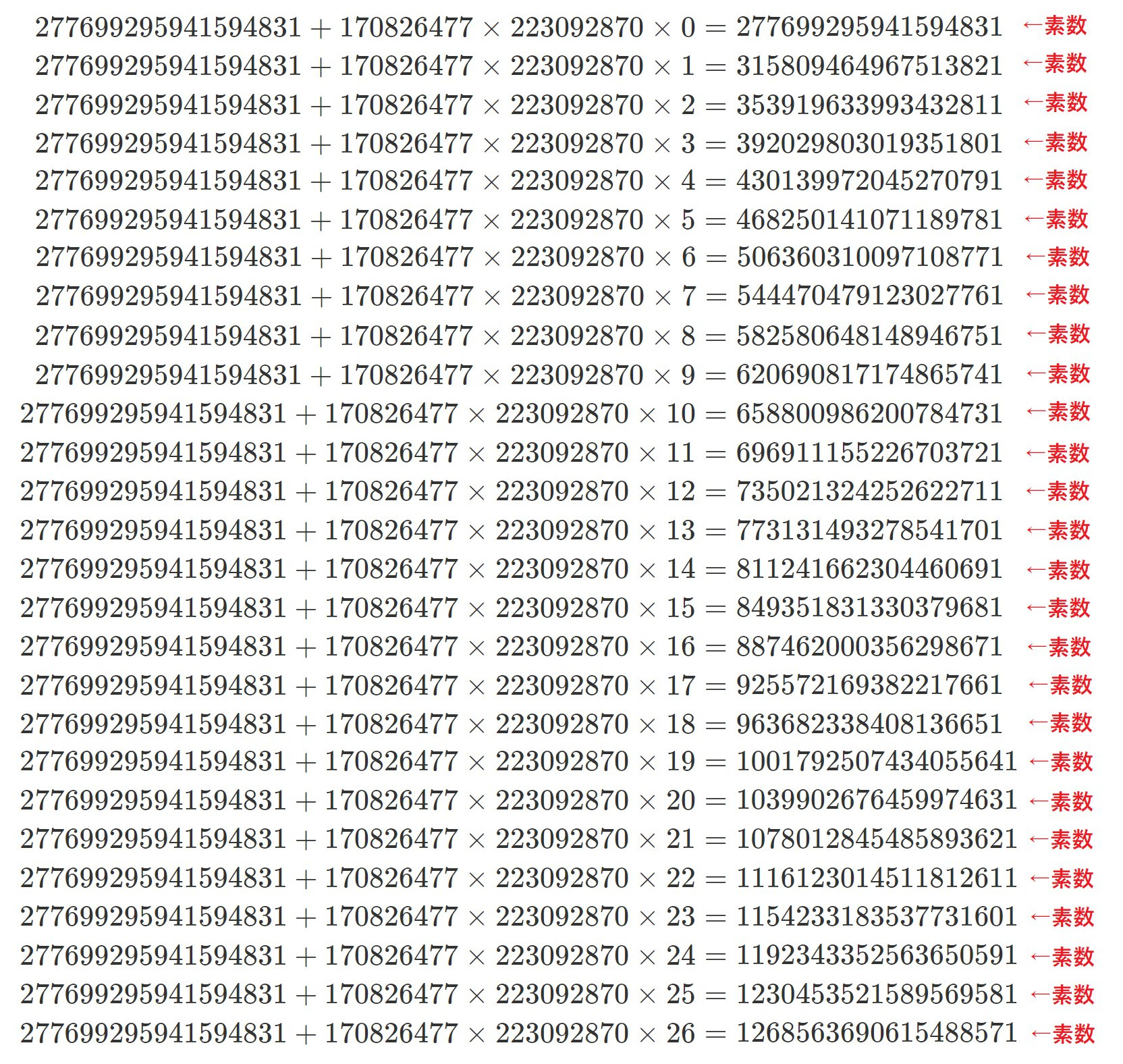
連続する27項が全て素数になるような等差数列が発見されました。

初項 $277699295941594831$, 公差 $170826477 \times 223092870 \  (= 38110169025918990)$ の等差数列です。

これまでに発見されている素数の等差数列の最長記録は 2019/9/23 に発見された長さ27項の

$$224584605939537911+81292139 \times 223092870 \times n \ \ \ \ (n = 0, 1, \cdots , 26)$$

で、今回発見された等差数列はそれに並ぶ最長記録タイです。

世界中の個人PCを繋いで協力して素数を探索するプロジェクトである PrimeGrid により今回の等差数列は発見されました。
(発見者：Tom Greer (America)　検証者：Vasil Zakiev (Russia) )

グリーン・タオの定理より素数の等差数列は任意の長さのものが存在しますが、実際には項数が多いものを見つけるのは難しく今回のように大人数が参加する分散コンピューティングで探索が続けられています。

(現在も、27項からなる素数の等差数列の探索プロジェクトは続いています：AP27 Search)

参考情報源

PrimeGrid 公式ニュースリリース：PrimeGrid’s AP27 Search
https://www.primegrid.com/download/AP-170826477.pdf

7月

3×2ⁿ - 1 型の最大の素数が発見される

(2023/7/5)

$3 \times 2^n - 1$ 型の素数の最大記録が更新されました。

6300184桁の素数で、発見当時は既知の素数全体の中でも19番目に大きい記録でした。
(2023/12/29現在、全体20位)

この素数も、世界中の個人PCを繋いで協力して素数を探索するプロジェクトである PrimeGrid により発見されました。
(発見者：Arno Lehmann (Germany))

参考情報源

PrimeGrid 公式ニュースリリース：PrimeGrid’s 321 Prime Search
https://www.primegrid.com/download/321-20928756.pdf

素数レコードサイト上での当該素数ページ
PrimePage：3・2 ^20928756 - 1

9月

フィボナッチ素数の最大記録が更新される(※暫定)

(2023/9/15)

フィボナッチ数のうち、素数であるもの(フィボナッチ素数)の最大記録が更新されました。

2023/9/15 に確率的素数判定法で素数判定されたのち、2023/11/9 に ECPP(elliptic curve primality proving：楕円曲線素数判定法) で実際に素数であると判明しました。

(注意：ECPP で素数性が示されたと報告されているのですが、素数レコードサイトにはECPPでの検証データが添付されておらず、検証ステータスが記録上は「PRP(確率的素数)」のままになっています。現時点では第三者が検証できない状態のため、暫定素数という表記にしました)

既知のフィボナッチ素数のランキングはこちらに掲載されています。
※確率的素数判定法で素数判定を受けただけで、まだ実際に素数性が証明されていないフィボナッチ数もランキングに掲載されています。(Verification status：PRPのもの)
※また、今回紹介したフィボナッチ素数も含め、ECPP で素数性が示されたものでも上記サイトに検証データが添付されていない物は Verification status が PRP(確率的素数)のままになっています。

参考情報源

素数レコードサイト上での当該素数ページ
PrimePage：U(201107)

フィボナッチ素数の記録一覧：Fibonacci Number
https://t5k.org/top20/page.php?id=39

10月

ワグスタッフ素数の最大記録が更新される(※暫定)

(2023/10/24)

ワグスタッフ素数の最大記録が更新されました。

(注意：ECPP で素数性が示されたと報告されているのですが、素数レコードサイトにはECPPでの検証データが添付されておらず、検証ステータスが記録上は「PRP(確率的素数)」のままになっています。現時点では第三者が検証できない状態のため、暫定素数という表記にしました)

ワグスタッフ素数とは、以下の形で表される素数です。
$$p=\frac{2^{q}+1}{3}$$
ただし、$q$ も素数です。

今回発見された素数は $q=138937$ に相当します。

新メルセンヌ予想に関連する素数であるため興味を持って探索されています。

参考情報源

素数レコードサイト上での当該素数ページ
PrimePage：(2¹³⁸⁹³⁷ + 1)/3

ワグスタッフ素数の記録一覧：Wagstaff
https://t5k.org/top20/page.php?id=67

12月

メルセンヌ数でない素数の最大記録が更新される

(2023/12/14)

$2^n - 1$ 型(メルセンヌ数) でない素数としては最大記録となる素数が今年10月(2023/10/2)に発見され、その後 12/14 に素数性の検証が完了しました。

(年末に素数ビッグニュース！！)

1198万1518桁の巨大な素数で、全体でも今まで発見された中で7番目に大きい素数です。

(素数判定プログラムでの検証には 約73.22日 ( (6326575.8607+1.4961) 秒 )を要していました。)

素数の形は、3番目の円分多項式 $x^2+x+1$ に $-516693^{1048576}$ を代入した形になっています。

そのためこの素数の素数データベース上の表記も「Phi(3, - 516693^1048576)」になっています。
※Phi(n, x) は n 番目の円分多項式に値 x を代入した数を表す

素数判定には N-1 test (Brillhart-Lehmer-Selfridge 素数判定法) が用いられたみたいです。(※これは決定論的アルゴリズムです)

現在の素数ランキングTOP20はこちらのページで確認できます。

本当にメルセンヌ数では無いのか

単に見た目が $2^n - 1$ に見えないというだけではメルセンヌ数でないことを示せていないので、実際にメルセンヌ数ではないことを確認してみます。

4 で割った余りがメルセンヌ数とは一致しないことから、本当に $2^n - 1$ の形で表すことができないことがすぐに分かります。

ちなみに、

なので、今回の巨大素数は $39801738$ 番目のメルセンヌ数と $39801739$ 番目のメルセンヌ数の間に存在します。

(隣り合うメルセンヌ数の間に存在するので、今回の素数がメルセンヌ数ではないことがこの不等式からも分かります)

参考情報源

素数レコードサイト上での当該素数ページ
PrimePage：Phi(3, - 516693^1048576)

2023 (月不明)

以下、おまけです。(適宜追加)

階乗数の積で表されるトリボナッチ数が全て決定される

上記内容の証明が 2023 に公開されました。

Alahmadi, Adel, and Florian Luca. "On Tribonacci Numbers that are Products of Factorials." Journal of Integer Sequences 26.2 (2023): 3.
https://cs.uwaterloo.ca/journals/JIS/VOL26/Luca/luca52.html
↑ページの「Full version: pdf」のリンクから論文のPDFに移動できます

トリボナッチ数が ある自然数の階乗になるのは $n$ が $1, 2, 3, 7$ の時だけであることは2014年に証明されていましたが、条件を緩めて 階乗の"積" で表される場合について検討されたのが上記論文です。

条件を緩めても $T_4 = 2!2!$ が追加されただけで、階乗数の積で表されるトリボナッチ数は有限個かつ初項近辺にしか存在しないことが明らかになりました。

※論文ではトリボナッチ数の初期値が $T_0=0, T_1=T_2=1$ になっていました。他の書籍での記述とのズレにご注意ください。