その際はタッチ操作で数式を横スクロールしてください
今年(2024)に目にした素数・整数関連のニュースを簡潔に一覧にしました。
素数・整数のトピックは適当に不定期で確認していただけなので、内容スカスカです…。(ごめんなさい)
(単に私が覚えているものをピックアップしただけなので重要な整数ニュースを多数見逃していると思います…。)
※私でも簡単に(表面を)理解できるような内容のものばかりで、専門的なトピックが含まれていません。
ニュースと言っておきながらジャーナルにはほぼ目を通していないので内容が「特定の形をした素数発見」みたいなものばかりです…。
なお素数に併記している日付は素数の発見日ではなく、基本的に素数データベース(PrimePages) での素数性検証完了日にしています。(発見日が公開された物は発見日で記載)
1月
回文素数の最大記録が連続で更新される
(2024/1/11)
$=\underbrace{99 \cdots 99}_{\text{948958 個}} \textcolor{red}{8}\underbrace{99 \cdots 99}_{\text{102087 個}} \textcolor{red}{8} \underbrace{99 \cdots 99}_{\text{948958 個}}$
$$(2,000,005 \ 桁)$$
(2024/1/17)
$=\underbrace{99 \cdots 99}_{\text{872812 個}} \textcolor{red}{8}\underbrace{99 \cdots 99}_{\text{254381 個}} \textcolor{red}{8} \underbrace{99 \cdots 99}_{\text{872812 個}}$
$$(2,000,007 \ 桁)$$
逆から数字を並べても同じ数になる素数である回文素数。
その最大記録が1月中に連続して更新されました。
いずれも「9」が数十万桁並ぶ中で 2 桁だけ「8」が含まれるような回文素数で、桁数は200万桁の大台を突破しています。
発見者はいずれも同一人物で、Serge Batalov さんです。
参考情報源
素数レコードサイト上での当該素数ページ
① PrimePages:10²⁰⁰⁰⁰⁰⁵ - 10¹⁰⁵¹⁰⁴⁶ - 10⁹⁴⁸⁹⁵⁸ - 1
② PrimePages:10²⁰⁰⁰⁰⁰⁷ - 10¹¹²⁷¹⁹⁴ - 10⁸⁷²⁸¹² - 1
回文素数の記録一覧:Palindrome
https://t5k.org/top20/page.php?id=53
2月
「9」だらけの巨大素数が発見される
(2024/2/7)
$=7 \underbrace{99999999999 \cdots 99999999999}_{\text{5112847 個}}$
$$(5,112,848 \ 桁)$$
先頭桁だけ「7」で、それ以降の数字が全て「9」で 511万2847個も続く巨大素数が発見されました。
このように、1つの桁を除いてすべての桁が同じ数字の素数は「near-repdigit 素数」(ニア-レプディジット素数)と呼ばれています。
(日本語にすれば「ほぼゾロ目素数」)
今回発見された「9」だらけの巨大素数は、near-repdigit 素数の中では史上最大記録です。
記録当時、素数全体で見ても38位の大きさでした。
見た目のインパクトが圧倒的です。
(発見者:Ryan Propper さん、Serge Batalov さん)
ㅤ
・repdigit とは、桁(digit) の 繰り返し(repeated) のこと。要はゾロ目。
・repdigit 数(ゾロ目数) のうち、素数になるのは「1」を繰り返した物のみ。
(※それ以外の数字のゾロ目だと結局 111…111 の倍数になるので素数ではない。例:777=111×7 )
・ゾロ目のうち一つの桁だけ別の数に変えれば素数になりうる。
・そのような素数が near-repdigit 素数 (ほぼ-ゾロ目素数)
※「1」を繰り返したゾロ目素数は「repunit 素数」(レピュニット素数) と呼ばれています。
参考情報源
素数レコードサイト上での当該素数ページ
PrimePages:8 · 10⁵¹¹²⁸⁴⁷ - 1
ほぼゾロ目素数の記録一覧:Near-repdigit
https://t5k.org/top20/page.php?id=15
3月
10進キネア素数の最大記録が更新される
(2024/3/29)
$$(4,665,949 \ 桁)$$
$(2^n+1)^2-2$ の形式で表される素数
ㅤ
$b$ 進キネア素数
$(b^n+1)^2-2$ の形式で表される素数
※ Kynea は人名ですが読みが分かりませんでした。ここではキネアと表記しています。
10進キネア素数の最大記録が更新されました。
桁数は 466万5949桁 で、素数全体で見ても記録当時48位の大きさでした。
今回の記録は10進キネア素数の最大記録であるだけでなく、任意の $b$ 進キネア素数の中でも最大記録でした。
(※素数ランキングを上から順に48番目まで全部見て確認)
キネア素数の記録や詳細については次のページにまとめられています。
リンク:Carol-Kynea prime - Prime Wiki
ページの更新が2022年で止まっていますが、当時の最大記録 $${(146^{276995}+1)}^2-2 \ \ \ (1,199,030 桁)$$ に比べると今回の記録は圧倒的に大きいですね。
なおこのページには似た形のキャロル素数 (Carol prime) についても記録が掲載されています。
$b$ 進キャロル素数:$(b^n-1)^2-2$
今回の素数の発見者は Ryan Propper さんです。
参考情報源
素数レコードサイト上での当該素数ページ
PrimePages:(10²³³²⁹⁷⁴ + 1)² - 2
Wikipedia
Kynea数
7月
素数階乗素数 (p#+1 型) の最大記録が23年ぶりに更新
(2024/7/27) ※PrimeGrid による正式な発見日
$=2 \times 3 \times 5 \times \cdots \times 4328927 + 1$
$$(1,878,843 \ 桁)$$
素数階乗素数に大きなブレイクスルーがありました。
素数階乗 $p\#$とは、$2$ から $p$ までの素数の積のことです。
素数階乗素数は、素数階乗に1足した数 $p\#+1$ または 1引いた数 $p\#-1$ のことで、今回 $p\#+1$ の方の記録が23年ぶりに更新されました。
$2$ から $4328927$ までの30万4723個の素数の積に $1$ を足した数で、23年前 (2001年) の記録 $$392113\#+1 \ \ \ (169,966 桁)$$ と比べて大きな飛躍です。
(発見者:Kai Presler さん)
p#+1 が素数になるのは当たり前?
$2$ から $p$ までの素数の積に $1$ を足した数なのだから $2$ から $p$ までの素数で割ると必ず $1$ 余るでしょ? と疑問の方…!
確かにその通りで $p$ までの素数では割り切れませんが、$p$ よりも大きな素数の積で表せる可能性が残っているため素数とは限りません。
(例:2~13までの素数の積に+1した数は素数ではない)
$$2 \times 3 \times 5 \times 7 \times 11 \times 13 + 1 = 30031 = 59 \times 509$$
むしろ $p\#+1$ が素数になってくれる $p$ は非常に限られていて、今回発見された $p=4328927$ 以下の範囲では $23$ 個しか発見されていません。
(オンライン整数列大辞典(OEIS):A005234)
貴重な発見です。
発見の経緯
この素数階乗素数は、世界中のPCを繋いで協力して素数を探索するプロジェクト PrimeGrid の素数階乗素数探索プロジェクト「PrimeGrid's Primorial Prime Search」で発見されました。
(このように、計算処理をネットワークを介して複数のコンピュータで分担して同時並行的に行うことは分散コンピューティングと呼ばれています)
発見者となった Kai Presler さんのマシンスペックは
- CPU:Intel Xeon CPU E7-8890 v4 @ 2.20GHz
- メモリ:256 GB
- OS:Linux Mint 21.1
で、素数判定ソフト PRST を用いて 6時間53分の計算時間で確率的素数であると判定しました。
その後実際に素数であることが検証され、晴れて素数記録として認定されました。
(決定的素数判定により素数性を検証するのに要した時間は 2日と3時間38分)
より詳細な発見の経緯は以下の参考情報源のプレスリリースに記載されています。
参考情報源
PrimeGrid の公式プレスリリース
PrimeGrid's Primorial Prime Search:4328927# + 1
素数レコードサイト上での当該素数ページ
PrimePages:4328927# + 1
素数階乗素数の記録一覧:Primorial
https://t5k.org/top20/page.php?id=5
素数階乗素数 (p#-1 型) の最大記録も3年ぶりに更新
(2024/7/31) ※PrimeGrid による正式な発見日
$=2 \times 3 \times 5 \times \cdots \times 4778027 - 1$
$$(2,073,926 \ 桁)$$
$p\#+1$ 型の素数階乗素数の記録更新に続いて、今度は $p\#-1$ 型の方の記録も更新されました。
$2$ から $4778027$ までの33万4023個の素数の積から $1$ を引いた数で、3年前 (2021年) の記録 $$3267113\#-1 \ \ \ (1,418,398 桁)$$ から大きく更新です。
発見者は $p\#+1$ の時と同じく Kai Presler さんですが、使用マシンは別の物でした。
- CPU:AMD EPYC 7662 64Core Processor @ 2.0GHz
- メモリ:64 GB
- OS:Linux Mint 21.1
素数判定ソフト PRST を用いて4時間34分の計算時間で確率的素数であると判定され、その後実際に素数であることが決定的素数判定法により検証されました。
参考情報源
PrimeGrid の公式プレスリリース
PrimeGrid's Primorial Prime Search:4778027# - 1
素数レコードサイト上での当該素数ページ
PrimePages:4778027# - 1
素数階乗素数の記録一覧:Primorial
https://t5k.org/top20/page.php?id=5
ビジービーバー関数 BB(n) の n = 5 の値が確定する
(2024/7/2)
$$BB(5) = 47176870$$
※ 今回のビジービーバー関数 $BB(n)$ は最大シフト数関数 $S(n)$ のことです。
つまり、$5$ 状態 $2$ 記号のチューリングマシンが停止せずに $47176871$ 回以上シフトした場合、そのチューリングマシンは (シフト回数が $BB(5)$ を超えているので) 決して停止しないことになります。
チューリングマシンを実際に動かせるシミュレーター付きの分かりやすい解説が以下のページに載っていたのでおすすめです!!
$5$ 状態 $2$ 記号のチューリングマシン (超超ざっくり)
※厳密な定義は完全にすっ飛ばしてます。(自分もろくに理解していない)
| マシンの状態 | セルの記号が「0」 | セルの記号が「1」 |
| A | 1RB | 1LC |
| B | 1RC | 1RB |
| C | 1RD | 0LE |
| D | 1LA | 1LD |
| E | --- | 0LA |
チューリングマシンは、各セルに記号「0」または「1」を書き込める無限長のメモリテープ上で動作する抽象的な(仮想上の)マシンです。
(メモリテープの記号の読み取りと、メモリテープへの記号の書き込みが可能)
チューリングマシンは複数の「状態」を持つことができ、状態によってセルから記号を読み取ったときの動作を変えることができます。
その規則を表したのが上記の表です。
例えばマシンが状態「A」で、セルから読み取った記号が「0」のとき、動作は「1RB」です。
つまり、
- そのセルを「1」に書き換える
- 読み取り位置を1つ右 (Right) の位置にシフトする
- マシンの状態を「B」に変える
これで読み取り位置が 1 つ右にシフトし、動作の 1 ステップが完了しました。
次のセルにも「0」が書き込まれていたとすると、今はマシンの状態が「B」なので動作は「1RC」、つまり
- そのセルを「1」に書き換える
- 読み取り位置を1つ右 (Right) の位置にシフトする
- マシンの状態を「C」に変える
になります。
この動作を繰り返し、最終的に動作が停止命令「---」になったらチューリングマシンは停止します。
(上記の表の場合、マシンの状態が「E」のときに記号「0」を読み取ったらマシンは停止する)
上記の表は $5$ 状態 $2$ 記号のチューリングマシンの1つの例であり、マシンの状態とセルの記号の組み合わせで $5 \times 2 = 10$ 個の動作規則を自由に指定する余地があります。
ビジービーバー関数で考える対象
(※ここでは、全てのセルにあらかじめ「0」が書き込まれているメモリテープを使い、マシンは状態「A」から始まるものとします。)
動作規則の設定によっては、チューリングマシンが無限ループ状態に陥りいつまでも停止しない場合があります。
そのようなチューリングマシンを除外し、停止するマシンだけを考えた際にシフト数が最大になるようなマシンの規則は何か、そしてそのシフト数がいくつになるか求めるのがビジービーバー問題です。
停止するあらゆる $5$ 状態 $2$ 記号のチューリングマシンの中で、停止するまでにシフトする回数の最大値 $BB(5)$ を求めるのが今回の問題でした。
実は先ほど表で示したチューリングマシンが、動作が停止するまでに $47176870$ ステップも要する $BB(5)$ 候補のマシンで、1989年にこれが発見されてから長らくこれを上回るシフト数のマシンは見つかっていませんでした。
そして2024年にようやく、実際にこのマシンのシフト数が上限値であることが示され、
$$BB(5) = 47176870$$が確定しました。
証明には証明支援システムの Coq が用いられ、こちらの GitHub リポジトリにコードが公開されているので誰でも証明を出力して検証できる状態です。
今後、証明を人間が読める論文の形で公表することを目的に研究が進められているようです。
情報源・気になる資料
$BB(5)$ を求めるビジービーバーチャレンジの公式達成報告
[July 2nd 2024] We have proved “BB(5) = 47,176,870”
ビジービーバー問題の分かりやすい解説 (チューリングマシンシミュレーター付き)
The Busy Beaver Challenge
今回のビジービーバー問題の進展についての面白い読み物
With Fifth Busy Beaver, Researchers Approach Computation’s Limits
ビジービーバー問題の Wiki
Wiki - bbchallenge
Wikipedia - ビジービーバー
ビジービーバー
8月
2ちゃんねらーが素数階乗素数の最大記録を更新
(2024/8/6) ※PrimeGrid による正式な発見日
$=2 \times 3 \times 5 \times \cdots \times 5256037 + 1$
$$(2,281,955 \ 桁)$$
先月記録更新があったばかりの素数階乗素数について、また記録が更新されました。
$2$ から $5256037$ までの36万5071個の素数の積に $1$ を足した数で、先月末の記録を爆速で塗り替えました。
発見者は日本の Itsuki Kadowaki さんで、Team 2ch の所属メンバーであることが公式プレスリリースに記載されています。
Team 2ch は分散コンピューティングに参加する2ちゃんねらーによって構成されたチームで、かつて UDがん研究プロジェクト (がん治療薬候補分子探索の分散コンピューティングプロジェクト) でチーム成績世界一位をキープし続けて話題になったこともあります。
現在も色々な分散コンピューティングプロジェクトに参加しているみたいで、この素数探索にも Team 2ch が貢献しています。
自分も Team 2ch のメンバーとして素数探索してみたい! という方は、以下のページに非常に詳しい説明があるのでご参照ください。
↑素数探索を行う上で知っておきたい基礎知識や、探索・発見の流れ、必要なソフトウェアの導入・設定方法など色々と詳しく記載されています。
参考情報源
PrimeGrid の公式プレスリリース
PrimeGrid's Primorial Prime Search:5256037# + 1
素数レコードサイト上での当該素数ページ
PrimePages:5256037# + 1
素数階乗素数の記録一覧:Primorial
https://t5k.org/top20/page.php?id=5
回文素数の最大記録が再び更新される
(2024/8/16)
$=\underbrace{99 \cdots 99}_{\text{1087142 個}} \textcolor{red}{4}\underbrace{99 \cdots 99}_{\text{543995 個}} \textcolor{red}{4} \underbrace{99 \cdots 99}_{\text{1087142 個}}$
$$(2,718,281 桁)$$
逆から数字を並べても同じ数になる素数である回文素数。
1月に最大記録の更新がありましたが、8月になって新たにより大きな物が素数データベースに登録され記録更新になりました。
「9」が数十万桁並ぶ中で 2 桁だけ「4」が含まれるような回文素数で、桁数は前回記録の200万7桁と比べて70万桁以上増加しています。
(発見者:Ryan Propper さん、Serge Batalov さん)
参考情報源
素数レコードサイト上での当該素数ページ
PrimePages:10²⁷¹⁸²⁸¹ - 5 · 10¹⁶³¹¹³⁸ - 5 · 10¹⁰⁸⁷¹⁴² - 1
回文素数の記録一覧:Palindrome
https://t5k.org/top20/page.php?id=53
k×2ⁿ - 1 型素数の最大記録が更新される
(2024/8/29)
$$(7,409,172 \ 桁)$$
$k \times 2^n - 1$ 型 ( $k$ は $3$ 以上かつ $2$ の冪でない) の素数の中で過去最大の物が発見されました。
素数記録全体で見ても、発見当時14位の記録の巨大素数です。
(発見者:Ryan Propper さん)
参考情報源
素数レコードサイト上での当該素数ページ
PrimePages:69 · 2²⁴⁶¹²⁷²⁹ - 1
素数階乗素数の記録更新ラッシュが発生
8月中に素数階乗素数の記録更新が他にも2つあったので、こちらにまとめます。
(偶然にも同日に発見)
(2024/8/12) ※PrimeGrid による正式な発見日
$=2 \times 3 \times 5 \times \cdots \times 6354977 - 1$
$$(2,758,832 \ 桁)$$
発見者:Tom Greer さん (アメリカ)
PrimeGrid の公式プレスリリース:リンク
素数レコードサイト上での当該素数ページ:リンク
(2024/8/12) ※PrimeGrid による正式な発見日
$=2 \times 3 \times 5 \times \cdots \times 6369619 + 1$
$$(2,765,105 \ 桁)$$
発見者:Nick Merrylees さん (オーストラリア)
PrimeGrid の公式プレスリリース:リンク
素数レコードサイト上での当該素数ページ:リンク
10月
過去最大の一般化フェルマー素数が発見
(2024/10/4)
$$(8,238,312 \ 桁)$$
$2^{2^n}+1$ の形式で表される素数
ㅤ
一般化フェルマー素数 (Fermat prime)
$b^{2^n}+1$ の形式で表される素数 $(b \geqq 3)$
一般化フェルマー素数の最大記録が更新されました。
桁数は 823万8312桁 で、素数全体で見ても記録当時13位の大きさでした。
見た目が一般化フェルマー素数っぽくないですが、以下の通りこの形式で表せるため該当します。
$$4 \times 5^{11786358}+1 = (2 \times 5^{5893179})^{2^1}+1$$
すなわち、$b=2 \times 5^{5893179}, \ n=1$ のケースです。
$n^2+1$ で表せる素数としても最大
平方数+1 の形で表せる素数としても、今回の素数 $(2 \times 5^{5893179})^2+1$ は最大の物になります。
※この素数より大きな既知の素数 13 個についてそれぞれ、$1$ を引いた数の平方剰余を考えてそれが平方数でないことを確認しました。
ちなみに「 $n^2+1$ の形で表せる素数が無限に存在するか?」は未解決問題で、ランダウの問題 (Landau's problems) と呼ばれている物のうちの一つです。
現時点で、$n^2+1$ の形で表せる "素数または半素数" は無限に存在することまで示されているみたいなので、あと一歩…!!
参考情報源
素数レコードサイト上での当該素数ページ
PrimePages:4 · 5¹¹⁷⁸⁶³⁵⁸ + 1
一般化フェルマー素数の記録一覧:Generalized Fermat
https://t5k.org/top20/page.php?id=12
★史上最大の素数が発見される
(2024/10/12) ※GIMPS による正式な発見日
$$(41,024,320 \ 桁)$$
過去最大の素数が発見されました!!!
$2^{136279841}-1$ はメルセンヌ素数で、桁数は 4102万4320桁。
元王者の素数 $2^{82589933}-1$ は 2486万2048桁 だったので、そこから約1600万桁も大きな素数が今回見つかったことになります。
(前回の記録は2018年なので約6年ぶりの記録更新)
桁数があまりに大きすぎて実感が湧かないので、この素数の先頭 24702 桁 を計算して、1枚の画像で表示してみました。
(画像は縮小されているので、各桁の数を見たい場合は拡大するか画像を新しいタブで表示してください)

4102万4320桁 を全て表示するには、この画像が合計1661枚も必要です。
A4用紙に印刷する前提なら、コピー用紙の厚みを 0.09 mm で計算すれば約 15 cm もの厚さになります。
巨大さに圧倒されます…。
なお、発見されたメルセンヌ素数としては52個目です。
(それ以前に未発見のメルセンヌ素数があるかどうか検証が完了していないため、52番目かどうかは現時点で不明)
素数の先頭・末尾10桁
末尾10桁:$9486871551$
既知の完全数も1つ増えた
このメルセンヌ素数の発見で既知の完全数も1個増えて52個になりました。
$$(82,048,640 \ 桁)$$
※ $2^n-1$ が素数ならば $2^{n-1} \times (2^n-1)$ は完全数。
なぜメルセンヌ素数なのか
メルセンヌ数にはリュカ–レーマー・テストという高速な素数判定法が適用できるため、他の形の素数よりも探索が効率的という背景があります。
これに基づき分散コンピューティングでメルセンヌ素数を大規模に探索するプロジェクト GIMPS が進行中で、多人数が参加した結果巨大素数が次々と発見されています。
以上の理由で、発見される巨大素数は特定の形で表される物 (効率的な素数判定法が存在する物) に偏っています。
※2024年末時点で素数ランキングTOP20のうち12個がメルセンヌ素数です。(1~7位を独占)
発見の経緯
このメルセンヌ素数は、世界中のPCを繋いで協力してメルセンヌ素数を探索するプロジェクト GIMPS (Great Internet Mersenne Prime Search:グレート・インターネット・メルセンヌ素数探索) で発見されました。
発見者は Luke Durant さんです。
Luke Durant さんは多数の GPU サーバーで GIMPS 用のソフト(計算処理) を実行するためのインフラを開発し、17カ国24箇所のデータセンター地域にまたがる数千の GPU サーバーの圧倒的計算力を活かして素数探索を実行していました。
計算が約1年ほど続けられた結果、2024年10月11日にアイルランドのダブリンにある NVIDIA A100 GPU の計算で $2^{136279841}-1$ が確率的素数であることが判明しました。
(確率的素数判定法である フェルマーテスト で、メルセンヌ素数の候補が探索されていました。)
そして、確定的な素数判定法である先述のリュカ–レーマー・テストにより改めて検証され、$2^{136279841}-1$ が素数であることが確定しました。
検証は複数人によって複数のマシン・ソフトウェア上で実施されました。
(検証者:使用ソフト:実行環境 の順で掲載↓)
- Aaron Blosser さん:Prime95:Intel CPU
- Luke Durant, James Heinrich, Serge Batalov, Ken Kriesel, Mihai Preda さん:PRPLL/GpuOwl:AMD / NVIDIA GPU
- Serge Batalov さん:Mlucas:Intel CPU
- Luke Durant, Serge Batalov さん:CUDALucas:NVIDIA GPU
※ちなみに NVIDIA GPU で素数判定を実行するためのソフト CUDALucas は日本人が開発に携わったみたいです。(山田 正一郎さん?)
なお、素数の公式な発見日としては確率的素数判定法が実行された日ではなく、リュカ–レーマー・テストが実行された日が選択されました。
より詳細な発見の経緯は以下の参考情報源のプレスリリースに記載されています。
参考情報源
GIMPS の公式プレスリリース
GIMPS Discovers Largest Known Prime Number: 2136,279,841-1
素数レコードサイト上での当該素数ページ
PrimePages:2¹³⁶²⁷⁹⁸⁴¹ - 1
メルセンヌ素数の記録一覧:Mersenne
https://t5k.org/top20/page.php?id=4
11月
一般化ウッダル素数の最大記録が更新される
(2024/11/17)
$$(5,045,259 \ 桁)$$
$n \times 2^n-1$ の形式で表される素数
ㅤ
一般化ウッダル素数 (Generalized Woodall prime)
$n \times a^n-1$ の形式で表される素数 ( $a \geqq 3$ かつ $n > a-2$ )
一般化ウッダル素数の最大記録が更新されました。
桁数は 504万5259桁 で、素数全体で見ても記録当時48位の大きさでした。
ウッダル数とは要は $2^n$ の係数と指数が同じ数になっているような整数 - 1 で、そのような数が素数であればウッダル素数と呼ばれます。
底を $2$ 以外にした物は一般化ウッダル数と呼ばれ、それも素数であれば同様に一般化ウッダル素数と呼ばれます。
(発見者:Ryan Propper さん、Serge Batalov さん)
参考情報源
素数レコードサイト上での当該素数ページ
PrimePages:5287180 · 3¹⁰⁵⁷⁴³⁶⁰ - 1
一般化ウッダル素数の記録一覧:Generalized Woodall
https://t5k.org/top20/page.php?id=45
12月
0~9 までの数字を綺麗に使った巨大回文素数が発見される
(2024/12/9)
ㅤ
$=10^{490030}+10^{309648}+12345678987654321 \times 10^{245007}+10^{180382}+1$
$$(490,031 \ 桁)$$
上記のように $0$ から $9$ までの数字を綺麗に使った面白い巨大回文素数が発見されました。
回文素数なので上から桁を見ても下から桁を見ても同じ並びになります。
桁数は 490,031 桁で、「9」を中央にして左右対称に並んだ形になっています。
中央の $12345678987654321 $ が芸術点高いですね!
なお、回文素数の中で現時点で 9 位の大きさです。
(発見者:Serge Batalov さん)
参考情報源
素数レコードサイト上での当該素数ページ
PrimePages:10⁴⁹⁰⁰³⁰ + 10³⁰⁹⁶⁴⁸ + 12345678987654321 · 10²⁴⁵⁰⁰⁷ + 10¹⁸⁰³⁸² + 1
回文素数の記録一覧:Palindrome
https://t5k.org/top20/page.php?id=53
階乗素数の最大記録が更新される
(2024/12/12)
$$(3,395,992 \ 桁)$$
今度は階乗素数で記録更新が起こりました。
階乗 $n!$ は $1$ から $n$ までの整数の積のことです。
階乗素数とは、階乗に1足した数 $n!+1$ または 1引いた数 $n!-1$ が素数である物のことで、今回 $n!-1$ の方の記録が2年ぶりに更新されました。
今年は階乗素数も素数階乗素数も記録更新があって凄い一年ですね。
(発見者:Ryan Propper さん)
参考情報源
素数レコードサイト上での当該素数ページ
PrimePages:632760! - 1
階乗素数の記録一覧:Factorial primes
https://t5k.org/top20/page.php?id=30
11~12月
いとこ素数の最大記録の更新ラッシュ
11月から12月にかけて、いとこ素数の記録が5連続で更新されました。
いとこ素数とは、差が $4$ である素数の組のことです。
(差が $2$ である素数の組が双子素数なので、双子より距離感がある感じですね)
記録はこちらのページで確認できます。
ここでは現時点で最大の物のみ記載します。
(2024/12/16)
p&= (74018908351 \times (2^{190738}−1)+4) \times 2^{95369}−1\\
p+4&=(74018908351 \times (2^{190738}−1)+4) \times 2^{95369}+3
\end{align*}
$$(86,138 \ 桁)$$
(発見者:Serge Batalov さん)
セクシー素数の最大記録の更新ラッシュ
11月から12月にかけて、セクシー素数の記録も連続で更新されました。
セクシー素数とは、差が $6$ である素数の組のことです。
記録はこちらのページで確認できます。
こちらも現時点で最大の物のみ記載します。
(2024/12/21)
p&= (84741735735 \times (2^{190738}−1)+4) \times 2^{95369}−1\\
p+6&=(84741735735 \times (2^{190738}−1)+4) \times 2^{95369}+5
\end{align*}
$$(86,138 \ 桁)$$
(発見者:Serge Batalov さん)
なお、今年更新されたいとこ素数記録×5個とセクシー素数記録×3個は全て Serge Batalov さんの記録です。(無双状態)
素数階乗素数の最大記録の更新ラッシュ
11月~12月に入っても素数階乗素数の記録更新は止まりませんでした。
今年発見された素数階乗素数は次の通りです。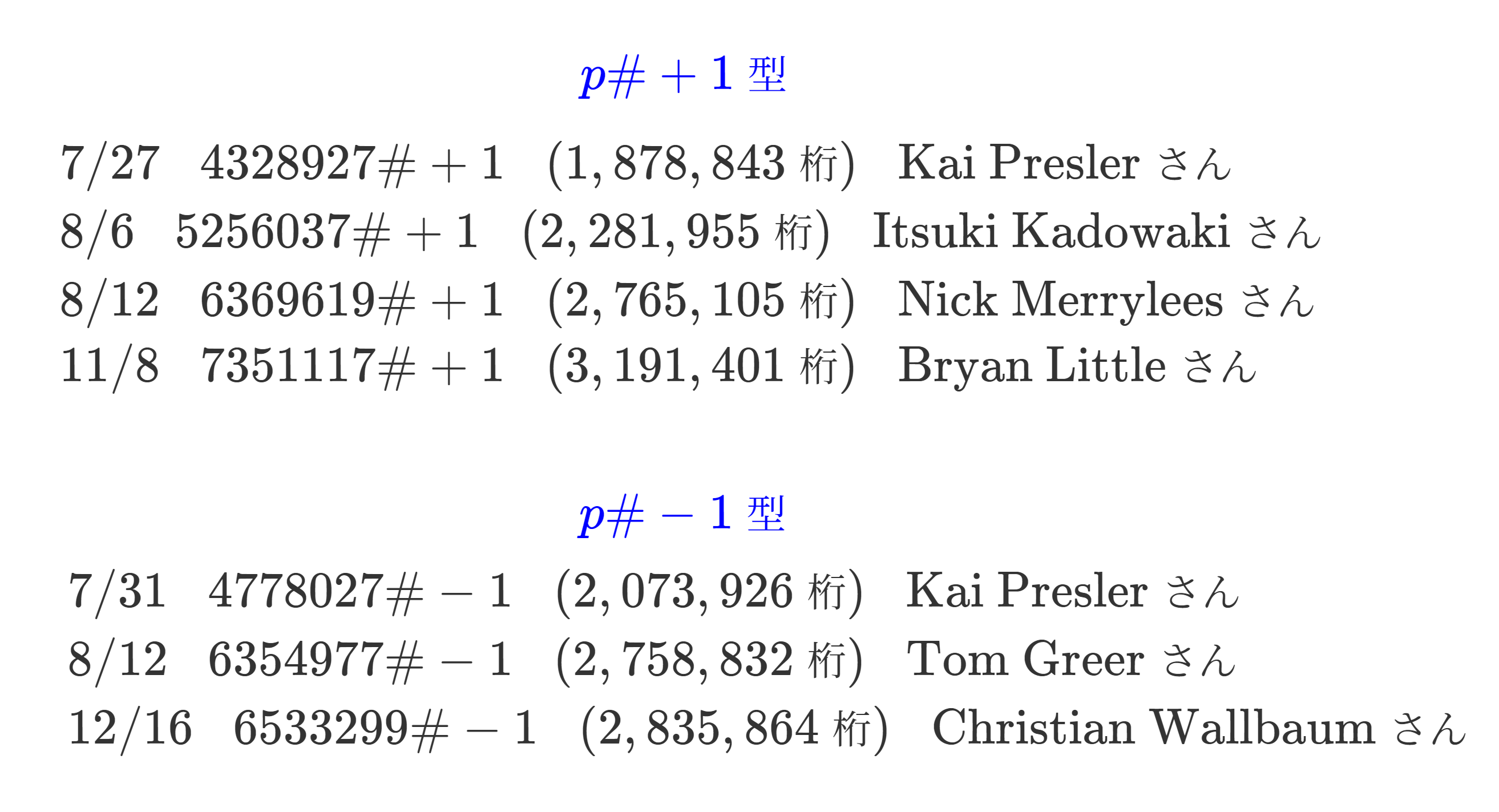
※日付は PrimeGrid の公式プレスリリースに記載されていた発見日に基づきますが、7351117#+1 と 6533299#+1 はまだプレスリリースが出ていなかったので PrimePages での素数性検証完了日を便宜上記載しています。
$p\#+1$ 型の最大記録 (2024年末時点)
(2024/11/8)
$=2 \times 3 \times 5 \times \cdots \times 7351117 + 1$
$$(3,191,401 \ 桁)$$
発見者:Bryan Little さん
素数レコードサイト上での当該素数ページ:リンク
$p\#-1$ 型の最大記録 (2024年末時点)
(2024/12/16)
$=2 \times 3 \times 5 \times \cdots \times 6533299 - 1$
$$(2,765,105 \ 桁)$$
発見者:Christian Wallbaum さん
素数レコードサイト上での当該素数ページ:リンク
素数ニュースバックナンバー
2023年の素数・整数ニュースもどうぞ!
[usemath] [sumaho] 今年(2023)に目にした素数・整数関連のニュースを簡潔に一覧にしました。 素数・整数のトピックは適当に不定期で確認していただけなので、内容スカスカです…。(ごめんなさい) (単に私[…]