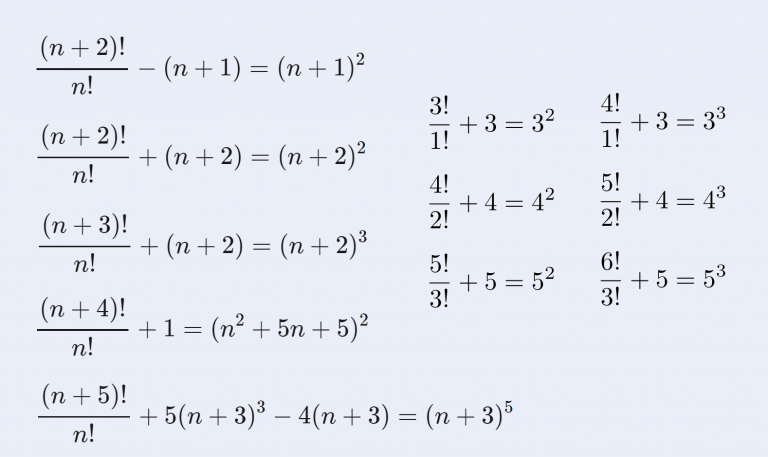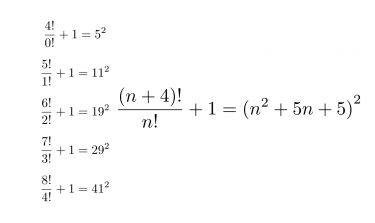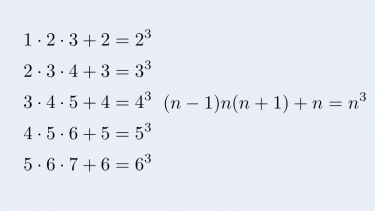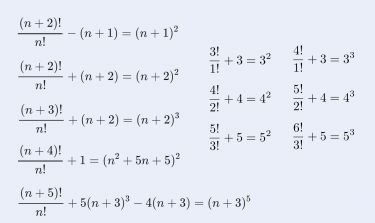その際はタッチ操作で数式を横スクロールしてください
前回の記事で、n+4 の階乗 と n の階乗の比 に 1を足すと平方数になることを示しました。
[usemath] [sumaho] 今回は、階乗が現れる恒等式を取り上げます。 次回の記事と併せてどうぞ! [sitecard subtitle=関連記事 url=https://pajoca.com/identity-o[…]
今回は差が4以外の場合について、何か綺麗な恒等式が成立しないか確かめてみます。
本記事集の数式一覧
n+1 の階乗 と n の階乗の比
これは単に
$$\frac{(n+1)!}{n!} = n+1$$
ですね…。
n+2 の階乗 と n の階乗の比
\frac{(n+2)!}{n!} &= (n+1)(n+2) \\
&= n^2+3n+2 \\
\end{align*}
なので、とりあえずこれを定数 $a$ を用いて平方数の形に直し、次に $a$ の値を調節してきれいな式を作ろうと思います。
\frac{(n+2)!}{n!} &= n^2+3n+2 \\
&= (n+a)^2 + (3-2a)n + 2-a^2 \\
\therefore \frac{(n+2)!}{n!} + (2a-3)n + a^2 -2 &= (n+a)^2
\end{align*}
$a=\frac{3}{2}$ のとき
となり左辺を簡単な形で表すことはできますが、分数が入ってしまって見た目がよろしくありません。
$a=1$ のとき
このとき、左辺と右辺の両方に共通の $(n+1)$ が出てきてきれいな形になりました。
具体的な整数を入れると、次のようになります。
$$\frac{3!}{1!} -2 = 2^2$$
$$\frac{4!}{2!} -3 = 3^2$$
$$\frac{5!}{3!} -4 = 4^2$$
$$\frac{6!}{4!} -5 = 5^2$$
$a=2$ のとき
このとき、左辺と右辺の両方に共通の $(n+2)$ が出てきてこちらもきれいな形になりました。
まだ2次式なので形を調整してきれいな形にしやすいですね。
具体的な整数を入れると、次のようになります。
$$\frac{3!}{1!} +3 = 3^2$$
$$\frac{4!}{2!} +4 = 4^2$$
$$\frac{5!}{3!} +5 = 5^2$$
$$\frac{6!}{4!} +6 = 6^2$$
n+3 の階乗 と n の階乗の比
\frac{(n+3)!}{n!} &= (n+1)(n+2)(n+3) \\
&= (n+2)\left\{(n+2)-1 \right\} \left\{(n+2)+1 \right\}\\
&= (n+2)\left\{(n+2)^2-1^2 \right\}\\
&= (n+2)^3 - (n+2)\\
\therefore \frac{(n+3)!}{n!} + (n+2)&=(n+2)^3
\end{align*}
と変形でき、今回は右辺が立方数になりました。
具体例は次のとおりです。
$$\frac{4!}{1!} +3 = 3^3$$
$$\frac{5!}{2!} +4 = 4^3$$
$$\frac{6!}{3!} +5 = 5^3$$
$$\frac{7!}{4!} +6 = 6^3$$
n+4 の階乗 と n の階乗の比
前回の記事で取り上げたとおり、
がなりたちます。
[usemath] [sumaho] 今回は、階乗が現れる恒等式を取り上げます。 次回の記事と併せてどうぞ! [sitecard subtitle=関連記事 url=https://pajoca.com/identity-o[…]
n+5 の階乗 と n の階乗の比
5次になると、なかなかきれいな形にするのは難しそうですね…。
式変形で、 $(n+3)$ を作りながら変形することで少しでもまとまった形にしようと思います。
\frac{(n+5)!}{n!} &= (n+1)(n+2)(n+3)(n+4)(n+5) \\
&= (n+3) \left\{(n+1)(n+5) \right\} \left\{(n+2)(n+4)\right\} \\
&= (n+3) \left\{(n+3-2)(n+3+2) \right\} \left\{(n+3-1)(n+3+1)\right\} \\
&= (n+3) \left\{(n+3)^2-2^2 \right\} \left\{(n+3)^2-1^2\right\} \\
&= (n+3) \left\{(n+3)^4-5 (n+3)^2+4\right\} \\
&= (n+3)^5-5 (n+3)^3+4(n+3) \\
\end{align*}
よってこの変形から、次の式が成り立つと分かります。
左辺を綺麗にすることは叶わず…。
具体例は次のとおりです。
$$\frac{6!}{1!} +5 \cdot 4^3 -4 \cdot 4= 4^5$$
$$\frac{7!}{2!} +5 \cdot 5^3 -4 \cdot 5= 5^5$$
$$\frac{8!}{3!} +5 \cdot 6^3 -4 \cdot 6= 6^5$$
$$\frac{9!}{4!} +5 \cdot 7^3 -4 \cdot 7= 7^5$$
4次までは綺麗に表せたのに…。
それでも、連続する整数の積はちょうど真ん中の整数を基準にして変形することで、展開せずに比較的きれいな式で表せることが確認できると思います。
これを利用して、等間隔の整数の積を綺麗に変形する方法について一般化したものがこちらです。
[usemath] [sumaho] 今回はタイトルで取り上げたような、連続する整数の積に成り立つきれいな等式について紹介しようと思います。ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ[…]
おわりに
今回は n+5 まで調べましたが、時間の有る方は n+6 以降も何か試してみてください。
高次になるにつれ式変形が大変になると思いますが😅
このように、階乗の比を含んだ式は変形して綺麗な恒等式を作れる場合があるので、もし面白い恒等式を作れた場合にはコメント欄で教えていただけると嬉しいです!!(๑ᴖ◡ᴖ๑)
コメント欄では数式も使えますので、お気軽にどうぞ!