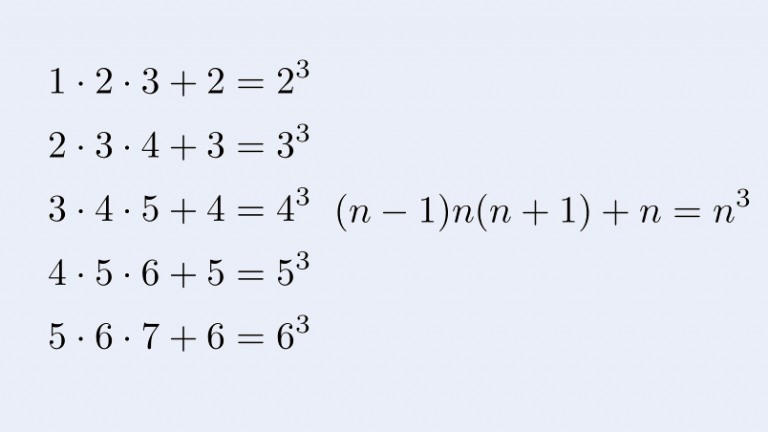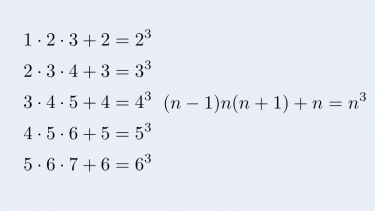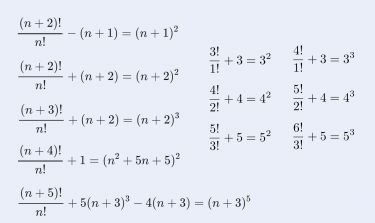その際はタッチ操作で数式を横スクロールしてください
今回はタイトルで取り上げたような、連続する整数の積に成り立つきれいな等式について紹介しようと思います。ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ
1\cdot 2 \cdot 3 +2&=2^3 \\
2\cdot 3 \cdot 4 +3&=3^3 \\
3\cdot 4 \cdot 5 +4&=4^3 \\
4\cdot 5 \cdot 6 +5&=5^3 \\
5\cdot 6 \cdot 7 +6&=6^3
\end{align*}
連続する3つの整数の積に真ん中の数を足すと、ちょうど真ん中の数の3乗になっていることが分かります!
今回はこのような綺麗な関係の等式が成り立つ理由や、これの一般化について書いていきます。
中学生でこの記事をお読みになっている方、記号として $3 \cdot 4$ などと $\cdot$ が現れますが、これはかけ算(積) $3\times 4$ のことです。
本記事の数式一覧
この記事で登場する式のまとめです。
連続する3つの整数の積
まずは冒頭で述べたような、3つの連続する整数のかけ算に成り立つ関係を見ていこうと思います。
3つの連続する整数の積は、整数 $n$ を用いて $(n-1)n(n+1)$ と表せます。
小さい方の数ではなく真ん中の数を $n$ とおくことで、式が対称的な形になり計算がたいへん行いやすくなります。
これを計算すると、
(n-1)n(n+1) &= n \left \{(n-1)(n+1) \right\} \\
&= n (n^2 -1) \\
&=n^3 -n
\end{align*}
となるので、
$$(n-1)n(n+1) + n = n^3$$
です。冒頭で述べた等式たちが必ず成り立つのはこのためです。
このように連続する整数の積は真ん中の整数を基準に考えると計算が楽になります。
これだけではつまらないので整数の間隔が広がった場合を考えます。
等間隔の3つの整数の積
$2\cdot 4 \cdot 6$ や $3\cdot 7 \cdot 11$ のような3つの等間隔の整数の積についてはどうでしょうか。
これも真ん中の数を基準にすることで簡単に計算できそうです。
3つの等間隔の整数の積は、真ん中の整数 $n$ と間隔 $a$ を用いて $(n-a)n(n+a)$ と表せます。(先程の連続する整数は $a=1$ の場合。)
こちらも
(n-a)n(n+a) &= n \left \{(n-a)(n+a) \right\} \\
&= n (n^2 -a^2) \\
&=n^3 -a^2 n
\end{align*}
となるので、
$$(n-a)n(n+a) +a^2 n = n^3$$
です。
具体的な整数を当てはめると、
1\cdot 3 \cdot 5 +2^2 \cdot3&=3^3 \\
2\cdot 4 \cdot 6 +2^2 \cdot4&=4^3 \\
3\cdot 5 \cdot 7 +2^2 \cdot5&=5^3 \\
\\
3\cdot 7 \cdot 11 +4^2 \cdot7&=7^3 \\
4\cdot 8 \cdot 12 +4^2 \cdot8&=8^3 \\
5\cdot 9 \cdot 13 +4^2 \cdot9&=9^3 \\
\end{align*}
のような感じになります。
等間隔の3つの整数の積に、「"間隔の2乗"×"真ん中の数"」を足してあげると、ちょうど真ん中の数の3乗になる訳ですね。
逆に言えば、等間隔の3つの整数の積は、間隔が広がるほど真ん中の数の3乗よりも小さな値になります。
この感覚を持っていれば、例えば $250 \times 300 \times 350$ よりも $300 \times 300 \times 300$ の方が大きいことがすぐ分かりますね!
等間隔の5つの整数の積
真ん中の整数を $n$ 、間隔を $a$ として計算すると、
(n-2a)(n-a)n(n+a)(n+2a) &= n \left \{(n-a)(n+a) \right\} \left \{(n-2a)(n+2a) \right\} \\
&= n (n^2 -a^2)(n^2 -4a^2) \\
&=n (n^4 -5a^2 n^2 + 4a^4) \\
&=n^5 -5a^2 n^3 + 4a^4 n
\end{align*}
となるので、
$$(n-2a)(n-a)n(n+a)(n+2a) +5a^2 n^3 - 4a^4 n = n^5$$
です。特に、5つの整数が連続している場合は $a=1$ なので
$$(n-2)(n-1)n(n+1)(n+2) +5n^3 - 4n = n^5$$
が成り立ちます。
残念ながら3つのときと比べると形があまり綺麗ではありません。
連続する5つの整数の積について、具体例は次のとおりです。
1\cdot 2 \cdot 3 \cdot 4\cdot 5 +5\cdot 3^3 -4\cdot 3&=3^5 \\
2\cdot 3 \cdot 4 \cdot 5\cdot 6 +5\cdot 4^3 -4\cdot 4&=4^5 \\
3\cdot 4 \cdot 5 \cdot 6\cdot 7 +5\cdot 5^3 -4\cdot 5&=5^5
\end{align*}
こんな感じで整数の積の個数が増えると形が綺麗ではなくなっていくので、今回は5つの整数の積まで考えました。
問題は式展開の途中で出てくる $n(n^2-1)(n^2-4)(n^2-9)\cdots$ が綺麗に表せないことで、この展開式は何か既存の知られている和Σの形に帰着できないのでしょうか…
何かご存じの方がいらっしゃいましたらコメント欄で教えていただけると嬉しいです!