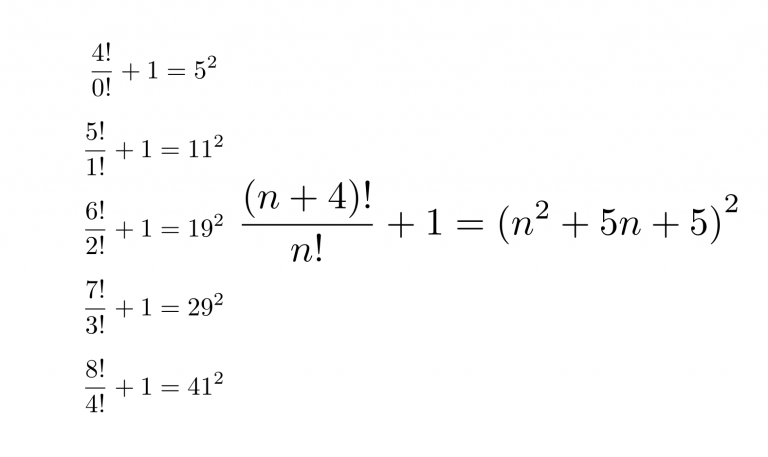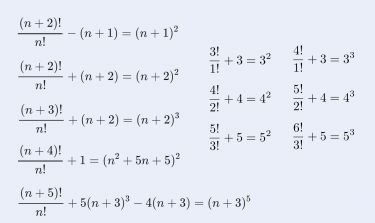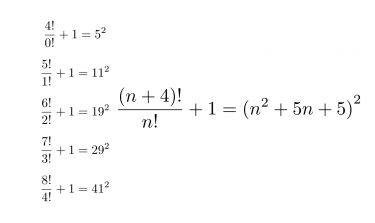階乗数の比に1足すと平方数になる | 階乗系の恒等式

整数 階乗の比に1を足すと平方数になる
スマートフォンでは、横長の数式が画面内に収まっていない場合があります
その際はタッチ操作で数式を横スクロールしてください

今回は、階乗が現れる恒等式を取り上げます。

次回の記事と併せてどうぞ！

関連記事
階乗の比に成り立つ関係と平方数・立方数 | 階乗系の恒等式

[usemath] [sumaho] 前回の記事で、n+4 の階乗 と n の階乗の比 に 1を足すと平方数になることを示しました。 [sitecard subtitle=関連記事 url=https://pajoca.com/i[…]

階乗を含んだ恒等式の一覧
目次

本記事の数式一覧

「n+4 の階乗 と n の階乗の比」以外の式は、上記の次回の記事にて取り上げています。

$$\frac{(n+2)!}{n!} -(n+1) = (n+1)^2$$
$$\frac{(n+2)!}{n!} +(n+2) = (n+2)^2$$
$$ \frac{(n+3)!}{n!} +  (n+2)=(n+2)^3$$
$$ \frac{(n+4)!}{n!} +1 = (n^2 + 5n +5)^2$$
$$ \frac{(n+5)!}{n!} +5 (n+3)^3-4(n+3)=(n+3)^5$$

n+4 の階乗 と n の階乗の比 に 1を足すと、平方数になる

予想される恒等式

$$\frac{4!}{0!} +1 = 5^2$$
$$\frac{5!}{1!} +1 = 11^2$$
$$\frac{6!}{2!} +1 = 19^2$$
$$\frac{7!}{3!} +1 = 29^2$$
$$\frac{8!}{4!} +1 = 41^2$$

ご覧のように、階乗数の比に1を足すと、綺麗に平方数になっています！

階乗をちょっといじるだけで、平方数を生成できるのです。

右辺の2乗される数は 5→11→19→29→41 と増加していますが、増加の度合いを見ると(階差をとると)

+6→+8→+10→+12 となっているので、2乗される数は2次式で表せそうです。

ということで、一般式は
$$\frac{(n+4)!}{n!} +1 = (n^2 + 5n +5)^2$$
と予想できます。

それでは、以下証明。(式変形で、成り立つことがすぐ分かります。)

証明

\begin{align*}
\frac{(n+4)!}{n!} +1 &= (n+1)(n+2)(n+3)(n+4)+1 \\
&= n^4 + 10n^3 + 35n^2 + 50n + 25 \\
&=(n^2 + 5n +5)^2
\end{align*}

計算のTips (受験生注目!)

上の証明では愚直に $(n+1)(n+2)(n+3)(n+4)$ を展開しましたが、実際には展開の仕方を工夫すると簡単に２乗の形に変形できます。

$(n+1)$ と $(n+4)$ 、$(n+2)$ と $(n+3)$ のペア(足して5になるペア) でかけ合わせると、共通の $n^2 + 5n$ を作れるところがポイントです。

\begin{align*}
\frac{(n+4)!}{n!} +1 &= (n+1)(n+2)(n+3)(n+4)+1 \\
&= \left\{(n+1)(n+4) \right\} \left\{(n+2)(n+3)\right\} +1 \\
&= (n^2+5n+4)(n^2+5n+6)+1 \\
&= \left\{(n^2+5n+5)-1 \right\} \left\{(n^2+5n+5)+1 \right\}+1 \\
&=(n^2+5n+5)^2 -1^2 +1 \\
&=(n^2+5n+5)^2
\end{align*}

すると、$(A-B)(A+B)=A^2 - B^2$ 型の展開に持ち込めるので、おだるい展開や因数分解なしに目的の形にたどり着けます。

この恒等式に関連する気になる問題

類似の階乗系恒等式は？　一般化可能？

差4 以外の階乗の比でも綺麗な恒等式が成立しないか？
$$\frac{(n+a)!}{n!} +k = (nの式)^N$$

今回の n+4 の階乗 と n の階乗の比の場合は1を足すだけで綺麗に平方数になりましたが、n+4 以外 の階乗の場合は綺麗に表せないでしょうか？

足す数は1でなくてもよく(ここでは $k$ とする)、右辺は平方数でなくてもよい ( $N$ 乗)ので、すっきりした形の恒等式が成立すれば嬉しいと思い試してみました。

しかし、4以外の場合についていろいろと考えてみましたが、階乗の比を単純な累乗で表すことはできませんでしたorz

何か成り立つ場合があったらコメント欄で教えていただけると嬉しいです！(｡^ω^｡)

もしかしたら1つの累乗ではなく累乗数の和で表せるかもしれません。

 

$$a! + b! = c! \times (綺麗な式)^N$$
が成り立つ他の例は？
今回の $\frac{(n+4)!}{n!} +1 = (n^2 + 5n +5)^2$ について、両辺に $n!$ をかけると
$$n! + (n+4)! = n! \times (n^2 + 5n +5)^2$$
となり、「階乗数＋階乗数＝階乗数×平方数」の形になります。
(この場合、$a=n, b=n+4, c=n$)
これを他の $a,b,c$ で考えて何か美しい等式を成立させることができないか気になります。
この場合、$a,b,c$ を特定の自然数として考えて、$a,b,c$ を求める整数問題として考えるのも面白そうです。
特定の整数で成り立つ場合が何かあったら教えてください！(๑ᴖ◡ᴖ๑)

階乗系の有名な整数問題

今回は階乗の"比"に1を足した平方数を考えましたが、階乗に1を足した時に平方数になるような整数の組が有限個かどうかを問う未解決問題「ブロカールの問題」があります。

$$n!+1=m^{2}$$
を満たす整数の組(n, m) は有限個か？　また、有限個だとしたら既知の $(n, m)=(4,5), (5,11), (7,71)$ 以外に解はないか？

階乗は少しいじると色々な整数問題へと発展するので大変面白いですね！

終わりに

今回は n+4 の階乗 と n の階乗の比について考えましたが、n+4以外 (n+2, n+3, n+5)の場合についても綺麗な式が得られるので、そちらも確認してみてください！

関連記事
階乗の比に成り立つ関係と平方数・立方数 | 階乗系の恒等式

[usemath] [sumaho] 前回の記事で、n+4 の階乗 と n の階乗の比 に 1を足すと平方数になることを示しました。 [sitecard subtitle=関連記事 url=https://pajoca.com/i[…]

階乗を含んだ恒等式の一覧
階乗の比に1を足すと平方数になる
記事化前の最新情報はこちらで先にツイートしています。サイト更新告知もこちら。

整数の最新記事8件